10. Графическое решение игр 2´2, 2´n, m´2

I). Пусть задана игра 2´2 платёжной матрицей

без седловой точки. Требуется найти оптимальные стратегии и цену игры n.

На оси абсцисс отложим единичный отрезок P2, P1. Каждой точке отрезка поставим в соответствие смешанные стратегии 1-го игрока , причём точка Р1 соответствует стратегии , точка Р2 стратегии . В точках Р1 и Р2 восстановим перпендикуляры I и II, на перпендикуляре II будем откладывать выигрыш 1-го игрока при стратегии P2, а на перпендикуляре I – при стратегии P1. Если второй игрок примет стратегию Q1, то она даёт выигрыш а11 при стратегии P1 и выигрыш а21 при стратегии P2. Отложим эти точки Q1 и На построенных перпендикулярах и соединим их отрезком прямой.

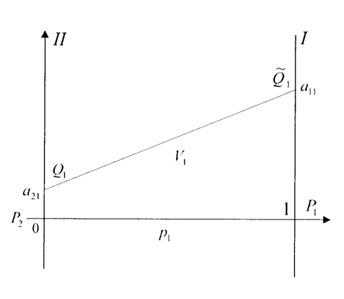
Рис.1

Средний выигрыш , соответствующей некоторой смешанной стратегии первого игрока, определяется точкой прямой с абсциссой . (2-ой игрок применил стратегию Q1). Пусть 2-ой игрок примет стратегию Q2. Аналогично строим отрезок . На перпендикуляре II отложим а22 – выигрыш первого игрока, если он выберет стратегию Р2; на перпендикуляре I отложим а12 – выигрыш первого игрока, если он выберет стратегию Р1. Полученные точки соединим прямой.

Рис.2

Средний выигрыш первого игрока, соответствующий его некоторой стратегии , определяется точкой этой прямой с абсциссой p1 (второй игрок применил стратегию Q2).

Известно, что первый игрок, придерживающийся своей оптимальной смешанной стратегии Р*, обеспечит себе выигрыш n, даже если второй игрок откажется от своей оптимальной стратегии.

Пусть n1 – средне ожидаемый выигрыш, полученный первым игроком при использовании смешанной стратегии против чистой стратегии второго игрока:

(1)

(согласно формулы (1) §2).

Пусть n2 – средне ожидаемый выигрыш первого игрока при использовании им смешанной стратегии против чистой стратегии второго игрока

(2)

Функции n1 и n2 – функции от p1, построим их графики – прямые, например по двум точкам - первую прямую и по точкам - вторую прямую.

Так как первый игрок может рассчитывать на выигрыш равный , то значения функции совпадают либо с n1 (при ), либо с n2 (при ).

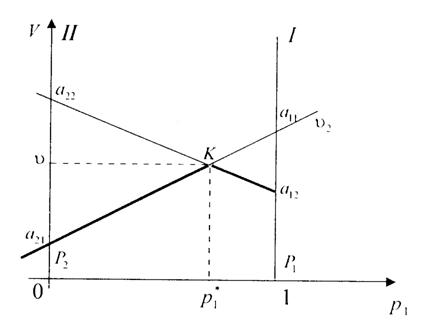
Рис.3

достигается в точке К (при ).

Таким образом, геометрический способ решения игры 2´2 заключается в построении прямых и определении точки К пересечения этих прямых Тем самым найдём цену игры n и оптимальную стратегию первого игрока Аналогично находим стратегии второго игрока.

Пример1. Решить матричную игру с платёжной матрицей

.

Решение. Седловой точки не существует (проверить самостоятельно). По точкам (0, -3), (1, 2) строим первую прямую (1) ; по точкам (0, 4), (1, -1) - вторую прямую (2)

Ломанная ВКА – нижняя граница выигрыша, (минимальный выигрыш первого игрока при применении им любых смешанных стратегий). Максимум функции достигается в точке К, т. е. минимальный (гарантированный) выигрыш достигает наибольшего значения при Тогда

Рис.4

Оптимальная стратегия I - го игрока цена игры Найдём оптимальную стратегию второго игрока

,

Строим прямые

Рис.5

Находим точку N – пересечения этих прямых.

Так как второй игрок может получить выигрыш то функция совпадает с n1, если или с n2, если

ВNA – верхняя граница выигрыша. Цена игры достигается в точке N при q1 = 0,5. Таким образом, оптимальная стратегия второго игрока Значит, первый игрок должен чаще применять первую чистую стратегию P1, второй игрок должен чередовать стратегию Q1 и Q2 с одинаковой частотой.

II). Игра M´2.

Пример 2. Найти решение игры, заданной платёжной матрицей А

Решение. Первая и четвёртая строки – доминируемые; вычеркнув их, получим матрицу игры: .

Одна сторона (1 игрок) имеет 4 стратегии, вторая сторона (второй игрок) имеет 2 стратегии. Седловой точки не существует. Суть геометрического способа поиска решения остаётся прежней. Строим прямые, определяемые уравнениями

Где - среднеожидаемый выигрыш второго игрока при использовании смешанной стратегии против чистой i-ой стратегии первого игрока ( - чистые стратегии первого игрока).

(1); (2) (3) (4)

У второго игрока может оказаться проигрыш .

Поэтому график функции - ломанная ВКМА:

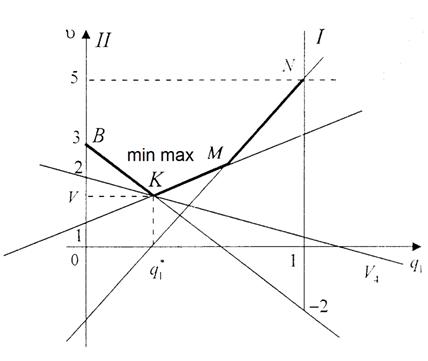
Рис. 6

Экстремальная точка К (минимакс) имеет координаты . Через точку К проходят три прямые, значит первый игрок имеет 3 активные стратегии из которых можно выбрать две, например (соответствующие прямые имеют разные наклоны).

Выбор исключён, т. к. точка К перестаёт быть экстремальной. Выберем, например, стратегии , которые включаем в игру 2´2. Игра приобретает вид .

Решая систему уравнений

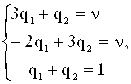
Получаем оптимальную смешанную стратегию второго игрока : и цену игры

Оптимальную стратегию первого игрока находим решая систему

Замечание: Игру 2´2 с платёжной матрицей 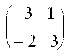можно было решить и графически.

Учитывая, что остальные чистые стратегии не представляют интереса как заведомо невыгодные, полагаем для них Таким образом, оптимальными стратегиями сторон являются

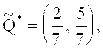
И учитывая отброшенные первую и четвёртую строки, получаем решение игры 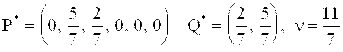, если первый игрок выбрал активные стратегии

Если первый игрок выберет активные стратегии тогда матрица игры приобретает вид (т. е. из матрицы А выбрали вторую и шестую строки, то оптимальные стратегии будут

Этот случай рассмотреть самостоятельно.

< Предыдущая		Следующая >