08. Матричные игры двух лиц с нулевой суммой в чистых стратегиях. Игра с седловой точкой

Раздел математики, изучающий конфликтные ситуации называется теорией игр. Конфликтные ситуации могут возникнуть в различных областях человеческой деятельности, например, арбитражные споры, рекламирование конкурирующих товаров, взаимоотношения между поставщиком и потребителем и т. п.

Для каждой игры вводятся:

1) правила, определяющие варианты ходов игроков;

2) объём информации о поведении партнёра;

3) выигрыш, к которому приводит совокупность действий.

Исход игры – значение некоторой функции выигрыша (количественной оценки выигрыша). Величина выигрыша зависит от стратегии игрока, т. е. совокупности правил однозначно определяющих последовательность действий игрока.

Наибольшее практическое значение имеют парные игры (конечные или бесконечные – в зависимости от количества стратегий). Конечные игры удобно представлять в матричной форме.

Игра с нулевой суммой – это игра, в которой общий капитал игроков не меняется, а лишь перераспределяется в ходе игры.

Решить игру – значит, для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, а именно: один из игроков должен получать максимальный выигрыш, когда второй игрок придерживается своей стратегии. При этом второй игрок должен минимизировать свой проигрыш, если первый игрок придерживается своей стратегии. Такие стратегии игроков называются Оптимальными.

Теория игр решает вопросы:

1) что считать оптимальным решением игры;

2) существуют ли оптимальные решения;

3) как найти оптимальные или близкие к ним решения.

Пусть первый игрок располагает M возможными стратегиями Р1, Р2,... Рm, принятыми игроком заранее. Назовём их Чистыми стратегиями. Первый игрок осуществляет выбор любой Pi стратегии (i = 1¸m) в каждой возможной ситуации (с учётом имеющейся информации). В ответ на Pi стратегию второй игрок может выбрать свою Qj чистую стратегию из N возможных стратегий Q1, Q2, ... Qn. Выбор стратегий любым игроком производится при полном незнании выбора другого игрока.

Если игра состоит только из личных ходов, то выбор пары стратегий (Pi, Qj) единственным образом определяет результат игры, aij – выигрыш первого игрока. При этом проигрыш второго игрока составляет +aij (т. е. второй игрок “выиграл”(- )) и сумма выигрышей обоих игроков будет равна aij + (-aij) = 0 (игра с нулевой суммой).

Если же существуют и случайные ходы, то исход игры обусловлен средним значением выигрыша.

Пусть aij известны. Составим матрицу игры – матрицу выигрыша первого игрока (или проигрыша второго игрока) A = {aij}, i=1¸m, j=1¸n. Матрицу А называют Платёжной. Платёжная матрица – табличная запись функции выигрыша.

Пусть оба игрока независимо друг от друга выбирают одну из своих чистых стратегий, т. е. пару (Pi, Qj), (первый игрок выбирает номера строк, а второй – номера столбцов матрицы А, ничего не зная о выборе противника). На пересечении i-ой строки и j-го столбца стоит элемент aij – выигрыш первого игрока (проигрыш второго). Цель игры – выбор наиболее выгодных стратегий, доставляющих первому игроку максимальный выигрыш, а второму – минимальный проигрыш.

Пример 1. Игра в отгадывание.

Пусть первый игрок имеет две карты: чёрную и красную. Из них он выбирает одну и не показывает противнику. Второй игрок называет цвет выбранной карты. Если он отгадал цвет карты, то первый игрок платит второму игроку 1р., если же второй игрок не отгадал цвет карты, то он платит первому игроку 1р. Составить платёжную матрицу.

Решение. Чистые стратегии первого игрока: выбор чёрной карты – P1 и выбор красной карты – P2. Чистые стратегии второго игрока: назвать чёрную карту – Q1 и назвать красную карту – Q2. Из выигрышей игроков составим платёжную матрицу А.

, здесь а11 = -1 – проигрыш первого игрока, если он выбрал свою первую чистую стратегию, и второй игрок выбрал свою первую чистую стратегию.

Аналогично определяем а12 = 1, а21 = 1, а22 = -1. Отметим, что, если применяются чистые стратегии важно, чтобы планы первого и второго игроков не были известны заранее.

Рассмотрим платёжную матрицу игры

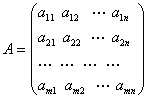
Первый игрок пытается найти наилучшую из своих стратегий, оценивая выигрыш поочерёдно для стратегии. Для стратегии P1 – гарантированным будет наименьший из элементов первой строки, для Р2 – наименьший из элементов второй строки и т. д. 2ой игрок будет стараться найти такую стратегию, которая сведёт выигрыш 1го к минимуму.

Ai = min Aij, 1 £ j £ n - минимально возможный выигрыш первого игрока, применяющего Pi стратегию для всех возможных стратегий Q1, Q2, ..., Qn второго игрока.

Наилучшей для первого игрока оказывается та стратегия, для которой ai максимальна: a = max ai, 1£ i £ m.

Число a называется Нижней чистой ценой игры (максимин),- гарантированный выигрыш первого игрока при любой стратегии второго игрока, а соответствующая ему чистая стратегия называется максиминной.

По каждому столбцу А определяется max Aij, bj = max Aij, - максимально возможный проигрыш второго игрока, если он пользуется стратегией Qj.

B = min bj = min max aij, - 1£ j£ n - верхняя чистая цена игры (минимакс).

Каждый игрок стремится достичь цели, противоположной цели противника, выбирая минимаксную или максиминную стратегии (правило минимакса). (Обще принятое условие: игрок, выбирающий строку, максимизирует платёж (выигрыш), а игрок, выбирающий столбец, минимизирует платёж).

Теорема 1. В матричных играх всегда a £ b.

Простейшим является случай, когда a = b т. е. в платёжной матрице существует элемент аij, который одновременно оказывается минимальным в i-ой строке и максимальным в j-ом столбце. Игра называется в этом случае вполне определённой или С седловой точкой; u = a = b - Чистая цена игры; ai*j* - седловой элемент платёжной матрицы.

Пару чистых стратегий (Pi*,Qj*), при которых a = b называют седловой точкой матричной игры. Стратегии Pi*, Qj* - оптимальные, они образуют решение игры.

В каждой игре с Седловой точкой (i*j*) первому и второму игрокам выгодно сохранять свои стратегии, отказ от принципа минимакса ведёт к увеличению проигрыша второго игрока и к уменьшению выигрыша первого игрока.

Пример 2. Каждый из двух игроков записывает одно из чисел 1,4,6,9. Затем они одновременно показывают написанное. Если оба числа оказались одинаковой чётности, то сумму чисел выигрывает первый игрок, если разной чётности - сумму чисел выигрывает второй игрок. Составить платёжную матрицу, найти нижнюю и верхнюю чистые цены игры и минимаксные стратегии.

Решение. Чистыми стратегиями первого игрока будут: записать Р1 – число1, Р2 – число 4, Р3 – число 6 и Р4 – число 9. У второго игрока чистыми стратегиями будут аналогичные стратегии. Элемент а11 = 2, т. к. в ситуации (P1,Q1) оба игрока записывают нечётное число 1 и выигрыш первого игрока = 1+1. Элемент а12 = -5, т. к. в ситуации (P1,Q2) первый игрок записывает число 1, а второй – число 4, т. е. числа разной чётности, поэтому выигрыш второго игрока = 5, а выигрыш первого игрока = -5 и т. д.

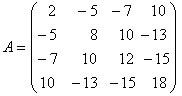
Составляем расширенную таблицу, в дополнительный столбец выписываем минимальный элемент каждой строки, в дополнительную строку – максимальный элемент каждого столбца.

	Стратегии 2го игрока
Стратегии 1го игрока	B1	B2	B3	B4	Ai
A1	2	-5	-7	10	-7
A2	-5	8	10	-13	-13
A3	-7	10	12	-15	-15
A4	10	-13	-15	18	-15
Bj	10	10	12	18	-7 10

Определяем a = maxai = -7 и b = min bj = 10, ; значит данная игра не имеет седловой точки.

Если 1 игрок выбирает первую стратегию, то может получить выигрыш 2, -5, -7, 10 в зависимости от выбранной стратегии второго игрока. Выигрыш будет не меньше min (2, -5, -7, -10)=-7.

Величина , будет гарантирным выигрышем игрока А, Нижняя цена игры.

Максимальной для первого игрока будет чистая стратегия P1 (первый игрок выиграет не менее –7, проиграет не более 7). Минимаксными для второго игрока будут чистые стратегии Q1 и Q2, при которых он проиграет не более 10 – верхняя цена игры.

Для любой матрицы , .

Пример 3. Решить матричную игру с платёжной матрицей:

Решение. Проверим, не имеет ли платёжная матрица седлового элемента

					Ai
	4	4	-3	3	-3
	-1	1	1	4	-1
	4	5	2	5	2
Bj	4	5	2	5	2 2

Находим a = max min aij = 2 и b = min max aij = 2, т. е. наименьший элемент третьей строки, равный 2, является одновременно наибольшим в третьем столбце, следовательно, матрица имеет седловую точку (3,3), а33=2. Значит, игра имеет решение в чистых стратегиях, а именно - оптимальная стратегия первого игрока, - оптимальная стратегия второго игрока. Цена игры u = 2.

Седловых точек может быть две или больше. Седловые точки взаимозаменяемые.

< Предыдущая		Следующая >