07. Задача сетевого планирования
Задача сетевого планирования является одной из важнейших задач, решаемых в условиях производства. Графический метод планирования применяется для визуализации организационно-управленческих процессов. С помощью сетевых графиков моделируются процессы реализации проектов. Сетевой график представляет собой множество вершин, соединённых между собой дугами. Каждая вершина представляет собой факт наступления определённого события, дуга символизирует выполнение работы. Каждой работе приписывают количественные характеристики (например время), необходимые для выполнения работы.
|
Основные понятия |
Определение |
|
Работа |
Один из главных элементов сетевой модели, означающий протяженный во времени процесс, требующий затрат ресурсов, или ожидание, или зависимость (фиктивная работа) |
|
Ожидание |
Протяженный во времени процесс не требующий затрат труда. |
|
Зависимость |
Логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени |
|
Путь |
Любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работой. |
|
Событие |
Момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. |
|
Полный путь |
Любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим. |
|
Предшествующий путь |
Путь от начала события до данного события сети. |
|
Следующий путь |
Путь, совершающий данное событие с завершающим событием сети. |
|
Критический путь |
Наиболее продолжительный путь в сетевом графике. |
Рассмотрим пример: необходимо построить сетевой график реализации проекта строительства здания и определить сроки реализации проекта. Перечень работ приведём в таблице.
Перечень работ по строительству здания
|
Работа |
Продолжительность выполнения, мес. | |
|
0-1 |
Проектирование здания |
2 |
|
1-2 |
Оформление заказа на строительные материалы и их получение |
2 |
|
1-3 |
Подготовка строительной техники и оборудования к работе |
1 |
|
1-4 |
Подготовка строительной площадки |
1 |
|
3-4 |
Рытьё траншей под фундамент |
2 |
|
4-5 |
Строительство здания |
4 |
|
3-7 |
Подведение коммуникаций |
1 |
|
4-6 |
Планировка и оформление придворовой территории |
1 |
|
7-8 |
Подключение коммуникаций |
1 |
|
5-8 |
Внутренняя отделка помещений |
2 |
|
6-8 |
Озеленение территории |
1 |
Для построения сетевого графика определим перечень событий:
0 – начало работ;
1 – готов проект здания;
2 – оформлен заказ и получены строительные материалы;
3 – строительная техника подготовлена к работе;
4 – подготовлена строительная площадка и вырыты траншеи под фундамент;
5 – возведено здание;
6 – проведена планировка и оформлена придворовая территория;
7 – проведены коммуникации;
8 – здание готово к эксплуатации.
На основе перечня событий и работ построим сетевой график.

Рис. 1
Числа над работами указывают их продолжительность.
Используя метод Форда вычисляем длиннейший путь графа, который определяет самую длительную технологическую цепочку, а следовательно кратчайший срок выполнения задания.

Рис. 2
На рисунке отмечены конечные метки для каждой вершины (работы) и критический путь, продолжительность которого равна 11 мес. Таким образом, ранний срок завершающего события равен 11 мес.
Работы в сетевом графике должны быть упорядочены по циклам (слоям). Существуют разные способы разбиения на слои. Например, можно выделить слои в графе исключением «потоков».
Пример. Дан граф. Требуется перенумеровать вершины графа.
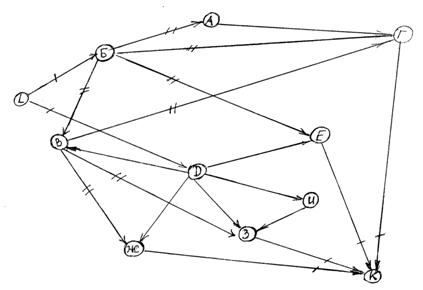
Рис. 3
1) Выделяем вершины, не имеющие предков (нет входящих дуг), определяем вершины из 1-го слоя (цикла). Это вершина ![]() . Вычеркиваем выходящие из вершины
. Вычеркиваем выходящие из вершины ![]() дуги. Получим подграф (граф без вершины
дуги. Получим подграф (граф без вершины ![]() ).
).
2) Выделяем в подграфе вершины, не имеющие предков (входящих дуг). Это вершины ![]() и
и ![]() . Они образуют 2-ой слой. Вычеркнем дуги, выходящие из вершин
. Они образуют 2-ой слой. Вычеркнем дуги, выходящие из вершин ![]() и
и ![]() и рассматриваем подграф (граф без вершин
и рассматриваем подграф (граф без вершин ![]() ,
, ![]() и
и ![]() ).
).
3) Вновь выделяем вершины, не имеющие входящих дуг. Это ![]() ,
, ![]() ,
, ![]() ,
, ![]() (образуют третий слой). Вычеркиваем дуги выходящие из этих вершин.
(образуют третий слой). Вычеркиваем дуги выходящие из этих вершин.
4) Далее находим вершины четвёртого слоя ![]() ,
, ![]() ,
, ![]() и в последний слой попадает вершина
и в последний слой попадает вершина ![]() .
.
Построим граф и перенумеруем вершины. Внутри слоя безразличен порядок нумерации. Вершины внутри каждого слоя не связаны.
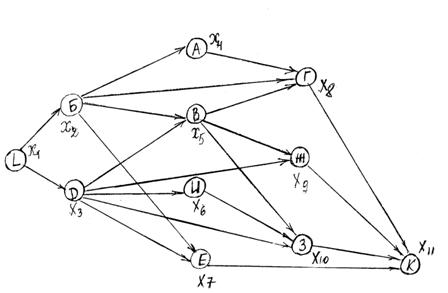
Рис. 4
Замечание.
Выделение слоёв можно начать с последнего слоя. Для этого находим вершины не имеющие потомков (нет выходящих дуг). Это вершина ![]() . Вычеркиваем все дуги входящие в вершину
. Вычеркиваем все дуги входящие в вершину ![]() .
.
Чтобы найти вершины предпоследнего слоя, выбираем вершины не имеющие потомков. Это вершины ![]() ,
,![]() ,
, ![]() ,
, ![]() . И т. д.
. И т. д.
Разбиение двумя способами может дать различные результаты.
Существует другой способ разбиения графа на циклы (слои).
Пусть граф задан в виде матрицы, элементы которой равны длинам дуг (продолжительности работ).
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
3 |
4 |
8 | ||||
|
2 |
2 |
4 | |||||
|
3 |
2 |
4 | |||||
|
4 |
3 |
1 |
4 | ||||
|
5 |
3 | ||||||
|
6 |
4 |
Составим матрицу смежности вершин, поставив в клетках ![]() единички, если существует дуга, идущая из вершины
единички, если существует дуга, идущая из вершины ![]() в вершину
в вершину ![]() .
.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
1 |
1 |
1 |
1 | ||||
|
2 |
1 |
1 | |||||
|
3 |
1 |
1 | |||||
|
4 |
1 |
1 |
1 | ||||
|
5 |
1 | ||||||
|
6 |
1 | ||||||
|
|
0 |
1 |
1 |
2 |
3 |
2 |
3 |
|
0 |
0 |
2 |
2 |
2 |
3 | ||
|
0 |
1 |
1 |
3 | ||||
|
0 |
0 |
2 | |||||
|
0 |
Сложим «1» по столбцам матрицы. Там где такая сумма равна нулю предков нет (нет входящих дуг). Это первый столбец. Вершина ![]() образует первый слой.
образует первый слой.
Вычеркиваем строку с номером «1» из матрицы и в новой матрице (имеющей теперь на одну строку меньше) вновь складываем «1» по столбцам. Второй и третий столбцы с нулевой суммой. Вершины ![]() и
и ![]() образуют второй слой. Вычеркиваем вторую и третью строки. Вершина
образуют второй слой. Вычеркиваем вторую и третью строки. Вершина ![]() Входит в третий слой. Аналогично находим четвёртый слой из вершин
Входит в третий слой. Аналогично находим четвёртый слой из вершин ![]() и
и ![]() . Вершина
. Вершина ![]() входит в последний слой.
входит в последний слой.
Замечание.
Разбиение на слои можно начать с суммирования «1» по строкам, с последующим вычеркиванием соответствующих столбцов. При этом на первом шаге определяем последний слой, затем предпоследний и т. д.
Задача, предлагаемая в задании 4 состоит из четырёх этапов:
1. Упорядочивание планируемых работ по производственным циклам.
2. Построение математической модели задачи в виде размеченного графа.
3. Поиск длиннейшего пути графа, которому отвечает самая длительная технологическая цепочка выполняемых работ, которая в свою очередь, определяет кратчайший срок выполнения всего производственного задания.
4. Анализ полученных результатов и определение возможных резервов для сокращения срока выполнения задания.
Поясним это на конкретном примере.
Задача. Составить сетевой график и определить минимальное время (в днях) выполнения производственного задания. Продолжительности (сроки) выполнения работ и последовательность их выполнения заданы в таблице (для каждой работы ![]() указано, после выполнения каких работ
указано, после выполнения каких работ ![]() Может быть начато её выполнение). Вместо названий работы задаются условно их номерами. Считается, что каждая работа начинается немедленно, как только появилась возможность.
Может быть начато её выполнение). Вместо названий работы задаются условно их номерами. Считается, что каждая работа начинается немедленно, как только появилась возможность.
|
Работа |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Срок |
20 |
30 |
18 |
19 |
45 |
14 |
28 |
19 |
32 |
29 |
|
После работ |
2, 4 |
- |
- |
15 |
2, 18 |
11,19 |
18 |
3, 19 |
6, 8 |
9 |
|
Работа |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Срок |
37 |
16 |
25 |
27 |
41 |
37 |
38 |
48 |
39 |
40 |
|
После работ |
4, 7 |
11,17 |
11 |
17 |
- |
8 |
1 |
- |
3 |
3, 7 |
Решение.
1) Введём две условные вершины: ![]() - отвечающую началу выполнения задания и
- отвечающую началу выполнения задания и ![]() - отвечающую завершению всех работ.
- отвечающую завершению всех работ.
Выполним разбиение на циклы способом описанном выше. Составим таблицу (матрицу) смежности (см. страницы 22 – 23)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 | |||||||||
|
| |||||||||||
|
|
1 |
1 | |||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
1 |
1 | |||||||||
|
|
1 |
1 | |||||||||
|
| |||||||||||
|
|
| ||||||||||
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 | |||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 |
1 | |||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
|
1 |
1 | |||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
| |||||||||||
|
|
1 | ||||||||||
|
| |||||||||||
|
|
|
| |||||||||
|
|
|
2) Для нахождения кратчайшего срока строим математическую модель задачи в виде размеченного графа (сетевой график). Для построения графа используются следующие правила:
а) вершины графа располагаются рядами в соответствии с циклами;
б) граф содержит две условные вершины: вершину ![]() , отвечающую началу выполнения задания (или завершению некой подготовительной работы 0), и вершину
, отвечающую началу выполнения задания (или завершению некой подготовительной работы 0), и вершину ![]() , отвечающую завершению всех работ;
, отвечающую завершению всех работ;
в) все остальные вершины графа обозначаются символами ![]() , где
, где ![]() ( по числу работ); вершина
( по числу работ); вершина ![]() отвечает завершению работы
отвечает завершению работы ![]() ;
;
г) две вершины ![]() и
и ![]() соединяются дугой в том и только в том случае, если работа
соединяются дугой в том и только в том случае, если работа ![]() непосредственно предшествует началу выполнения работы
непосредственно предшествует началу выполнения работы ![]() ; считается, что работа 0 предшествует работам нулевого цикла; фактически начала дуг указываются в третьей строке таблицы, а концы – в первой;
; считается, что работа 0 предшествует работам нулевого цикла; фактически начала дуг указываются в третьей строке таблицы, а концы – в первой;
д) длина дуги ![]() -
- ![]() полагается равной сроку выполнения работы
полагается равной сроку выполнения работы ![]() ;
;
е) вершины, соответствующие концам технологических цепочек, соединяются с вершиной ![]() условными дугами нулевой длины (на графике эти дуги показаны пунктиром).
условными дугами нулевой длины (на графике эти дуги показаны пунктиром).
Таким образом, мы получаем направленный размеченный граф, а точнее – сеть. Граф для нашей задачи изображен на рисунке.
3) Следующим этапом решения задачи является определение длиннейшего пути в построенном графе. Эта задача может быть решена методом меток Форда.
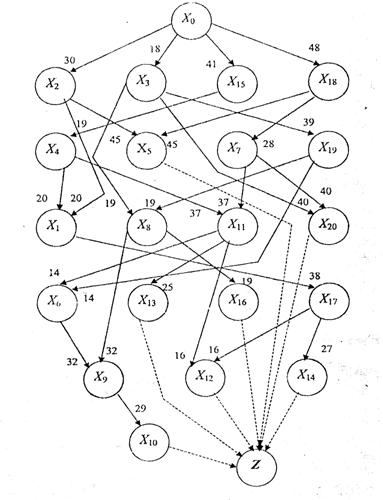
Сетевой график задания
4) Расчет временных характеристик проектов.
Рассмотрим следующие временные характеристики событий и работ:
1. Ранние сроки свершения событий ![]() :
:
2. Поздние сроки свершения событий ![]()
3. Резервы времени событий ![]()
4. Продолжительность критического пути ![]()
Пусть продолжительности работ ![]() строго детерминированны. Ранний срок свершения
строго детерминированны. Ранний срок свершения ![]() -го события
-го события ![]() (или ожидаемый) – наиболее раннее время относительно начала выполнения комплекса работ, когда может свершиться это событие.
(или ожидаемый) – наиболее раннее время относительно начала выполнения комплекса работ, когда может свершиться это событие.
Р. С.С. С. численно равен продолжительности максимального из путей, предшествующих этому событию от начального события до данного. Для определения Р. С.С. С. можно использовать алгоритм Форда.
1. Для начального события ![]() .
.
2. Для любого следующего события выбирается максимальный путь по всем его предкам по формуле ![]() .
.
Ранние сроки завершающего события равны длительности максимального пути (критического пути).
В сети может быть несколько критических путей.
Поздний срок свершения события – предельное по отношению к началу выполнения комплекса работ время свершения данного события, не влияющее на срок завершения проекта.
ПССС равен разности между длиной критического пути и продолжительностью максимального из путей от данного события до завершающего и может быть вычислено по алгоритму Форда в обратную сторону по формуле
![]()
Резерв ![]()
![]() -го события
-го события ![]() показывает на какой допустимый период
показывает на какой допустимый период ![]() можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.
Критические события резервов ![]() не имеют.
не имеют.
Ранний срок первого события равен ![]() .
.
Вычислим резервы времени для сокращения срока выполнения задания на следующем примере.
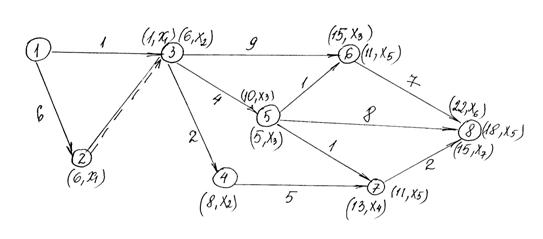
Так как ![]() , то получаем
, то получаем
![]()
![]()
![]()
![]()
![]() критическое равно 22
критическое равно 22
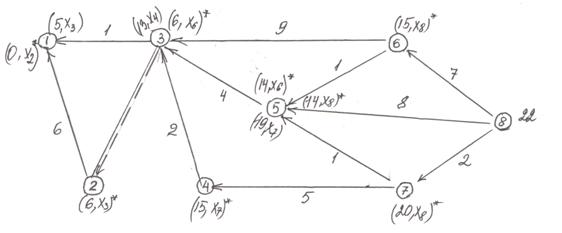
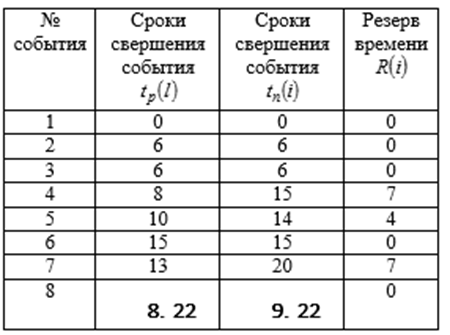
Для определения поздних сроков свершения событий двигаемся по пути в обратном направлении и используем формулу
![]() .
.
События с нулевыми резервами времени образуют критический путь.
| < Предыдущая | Следующая > |
|---|