06. Задача о кратчайшем пути в графе
Граф – совокупность 2х конечных множеств: вершин и ребер (или дуг).
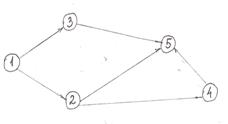
Не ориентированный граф Ориентированный граф
Ребрам придают некоторые числовые значения, например расстояния, время, пропускная способность и т. п.
Путь в ориентируемом графе – последовательность сцепленных ориентированных дуг, в которых начало каждой следующей дуги совпадает с концом предыдущей.
Цикл
В неориентированном графе цикл называют контуром.
Граф может быть задан в матричном виде
|
|
В графике не должно быть
А) тупиковых событий (не выходит ни 1 стрелки, за исключением последнего события);
Б) хвостовых событий (не предшествует ни одна вершина, за исключением первого события);
В) циклов;
Г) петель; 
Д) 2х стрелок 
Найти кратчайший путь в графе, значит указать упорядоченный набор дуг графа, в котором начало каждой следующей дуги совпадает с концом предыдущей, например 
или 
.
Каждой дуге 
сопоставляется целое неотрицательное число 
, называемое длинной этой дуги. Длина пути – сумма длин всех дуг, составляющих этот путь.
Для решения задачи о кратчайшем пути применяется алгоритм Форда, заключающейся в присвоении каждой вершине 
графа двойной метки 
, 
- некоторое число и в дальнейшем изменении этих меток. Рассмотрим работу алгоритма Форда на примере.
Пример.
1. Начальный шаг алгоритма.
Выделенной вершине 
присваивается метка 
и поставим рядом *, то есть 
и назовём такую метку Конечной, а вершину – Помеченной.
2. Общий шаг (повторяется многократно).
Рассмотрим все дуги, выходящие из отмеченной (помеченной) вершины. На первом шаге отмеченная вершина это вершина . Вычислим метки для вершин, в которые ведут дуги из : 
- это сумма метки и длины дуги, ведущей из в вершину 
. Из всех меток, которые получит вершина , выбираем наименьшую, отмечаем её * и считаем конечной. Повторяем общий шаг для определения конечных меток для всех вершин.
Рассмотрим работу Форда на примере.
Построить граф, заданный таблицей и найти кратчайший путь из в 
.
|
|
0,1 |
0,2 |
1,3 |
1,4 |
1,6 |
2,3 |
2,5 |
2,6 |
3,7 |
4,6 |
4,8 |
5,7 |
6,8 |
7,6 |
7,8 |
|
|
10 |
11 |
8 |
23 |
12 |
4 |
6 |
18 |
13 |
9 |
15 |
8 |
13 |
8 |
17 |
Из вершины выходят 2 дуги, ведущие в вершины 
и 
с длинами 
, 
.
Из ведут 3 дуги в 
, 
и 
и т. д.
Построим граф
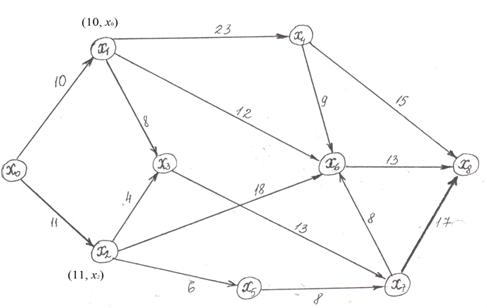
Рис. 1
Начальный шаг (применяется однократно).
Вершине присваивается метка . Вершину считаем помеченной.
Общий шаг.
1) Вершина имеет конечную метку. Из неё выходят 2 дуги в и . Вычисляем две метки 
и 
и записываем их рядом с вершинами и . Соответственно других дуг, ведущих в и нет, поэтому эти метки конечные, отмечаем их * и изобразим две конечные (окончательные) метки на рис. 1.
2) Вершина имеет конечную метку. Из неё выходят 3 дуги, ведущие в 
, , и .
Вычисляем соответствующие метки 
, 
, 
, 
и 
, 
. Так как в вершину больше не входит других стрелок, то и метка для вершины окончательная.
Изобразим вычисленные три метки для , , и на рис. 2. Вершина имеет конечную метку. Из неё выходят 3 стрелки в , 
, и . Вычисляем метки: 
для вершины , 
для вершины и 
для вершины .
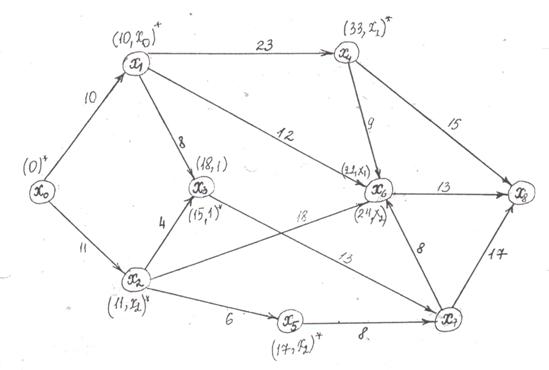
Рис. 2
В вершину не входят другие дуги. Из двух меток вершины выбираем наименьшую, это метка 
, она окончательная. Изобразим метки вершин , , и на рис.2, причем окончательные метки вершин и отмечаем *.
3) Вершина имеет конечную метку, из неё выходит единственная дуга в 
. Для получаем метку 
, т. е. 
, она не окончательная.
Из вершины в вершину идёт дуга, 
. Вычислим метку 
.
Вершина имеет окончательную метку.
Из двух меток вершины выбираем меньшую, это 
, она окончательная. Изобразим на рис. 3.
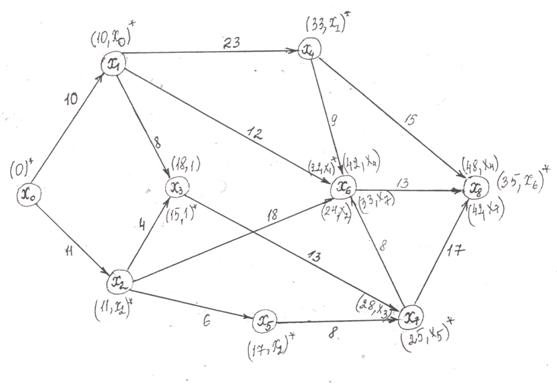
Рис. 3
4) Вершина имеет конечную метку, из неё ведут две дуги, вычисляем соответствующие метки 
в и 
в . Для вершин уже вычислены две метки. Из трех вычисленных меток , 
, выбираем меньшую и отмечаем её *.
Далее повторяем общий шаг пока не рассмотрим все оставшиеся вершины. При этом вершина получит окончательную метку *, вершина - 
*.
Двигаясь из в по помеченным меткам, получим кратчайший путь из вершины в вершину
и путь 
единиц.
Кратчайший путь из в равен 15, 
.
Также можно найти кратчайшие пути из в любую вершину 
, они равны окончательной метке вершины
| < Предыдущая | Следующая > |
|---|
