45. Дифференцирование функций многих переменных

Пусть функция векторного аргумента задана в некоторой области и пусть – некоторая точка этой области. Функция называется Непрерывной в точке , если для любого числа существует такое число , что из неравенства следует неравенство .

Пусть функция векторного аргумента задана в некоторой области и пусть – произвольная точка этой области. Придадим переменной приращение такое, чтобы было , где – Орт оси , представляющий собой вектор с -той единичной проекцией и остальными нулевыми проекциями. Вычислим разность и составим отношение . Если существует предел

,

То он называется Частной производной функции по переменной в точке и обозначается .

Итак, по определению

.

Частные производные вычисляются по обычным правилам и формулам дифференцирования, причем при вычислении дифференцирование ведется по переменной , а остальные переменные считаются неизменными.

Частные производные функции двух переменных геометрически представляют собой тангенсы углов наклона касательных к сечениям графика этой функции плоскостями и .

Если для функции в точке существуют все частные производные первого порядка, то она называется Дифференцируемой в точке . Если функция дифференцируема в точке , то она и непрерывна в этой точке.

Пусть функция является дифференцируемой при всех . Тогда она называется Гладкой.

Вектор-столбец частных производных функции в точке называется Градиентом и обозначается

.

Символ «набла» служит для обозначения оператора градиента . Градиент также обозначается через . Вектор градиента определяет направление наиболее быстрого возрастания функции в данной точке.

Поскольку по определению градиента , то

.

Если векторы-столбцы и зависят от , то по правилу производной произведения функций

.

Пусть функция имеет частные производные , . Предположим, что эти частные производные в свою очередь дифференцируемы по всем переменным. Тогда, дифференцируя по , получим Частную производную второго порядка функции по переменной . Она обозначается .

Дифференцируя по другой переменной , получим Смешанную частную производную второго порядка, которая обозначается

.

Теорема Шварца. Пусть функция имеет в точке и в некоторой ее окрестности частные производные

, , , .

Тогда

.

Пусть функция является дважды дифференцируемой по всем переменным. Тогда для такой функции можно составить матрицу вторых частных производных, которая называется Матрицей Гессе

.

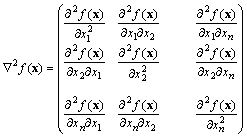В силу теоремы Шварца

, , .

Поэтому матрица Гессе является симметрической матрицей и для нее

.

Матрица Гессе также обозначается как .

< Предыдущая		Следующая >