42. Элементы векторной алгебры

Вектором называется упорядоченное множество действительных чисел. Например, , где , , …, действительные числа, есть вектор, состоящий из элементов. Количество элементов называется Размером вектора. Числа , , …, называются Проекциями вектора.

Два вектора и называются Равными, если равны все их соответствующие проекции: , . В этом случае пишут .

Если и то определены операции сложения и вычитания векторов:

,

.

Для любой скалярной величины определена операция умножения вектора на скаляр .

Вектор называется нулевым вектором.

Векторы , , …, называют Линейно зависимыми, если существуют скаляры , , …, , не все равные нулю, что

.

В этом случае хотя бы один из этих векторов можно представить Линейной комбинацией остальных векторов, например, при

.

В противном случае векторы называют Линейно независимыми.

Множество всех -мерных векторов называется -мерным Векторным пространством и обозначается . Говорят, что векторное пространство Натянуто на некоторую систему векторов, если каждый вектор из можно представить в виде линейной комбинации этой системы. Базис векторного пространства определяется как система линейно независимых векторов. Элемент пространства также называется Точкой. В этом случае , , …, называются Координатами точки.

Скалярное произведение двух векторов есть число, равное

.

Евклидова норма вектора определяется равенством

И соответствует длине вектора. Ее также обозначают и называют Модулем вектора.

Если векторы и рассматриваются как направленные отрезки, между которыми угол , то

.

Векторы называют Ортогональными И пишут , если .

Для векторов справедливо неравенство Коши – Буняковского – Шварца

.

Здесь равенство возможно только при .

Евклидова норма также называется -нормой и обозначается . В векторном анализе применяются -норма и -норма:

, .

Представленные нормы векторов – частные случаи -нормы

.

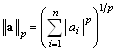Любая норма вектора обладает свойствами:

1)  , тогда и только тогда, когда ;

2)  , ;

3) , – неравенство треугольника.

Две нормы и называются Эквивалентными, если существуют такие, что

.

В частности,

, ,

, .

Таким образом, нормы , и являются эквивалентными.

Расстоянием между двумя точками и пространства называется евклидова норма разностей их координат

.

Расстояние обладает свойствами:

1) , тогда и только тогда, когда ;

2) ;

3)  – неравенство треугольника.

Последовательность векторов называется Сходящейся к вектору , если

.

Понятие сходимости последовательности векторов положено в основу исследования скорости сходимости методов многомерной оптимизации.

< Предыдущая		Следующая >