35. Свойства метода Девидона-Флетчера-Пауэлла

Эффективность метода ДФП определяется его свойствами.

Свойство 1. Если в формуле ДФП (4.20) матрица симметрическая, то матрица также симметрическая.

Доказательство. Пусть матрица симметрическая, то есть . Тогда, по формуле ДФП (4.20) с обозначениями , , , придем к формуле (4.19). Используя свойства матриц, получим:

.

Следовательно, . 

Свойство 2. Если в формуле ДФП (4.20) матрица положительно определенная и , то матрица также положительно определенная.

Доказательство. Пусть матрица положительно определенная и . Тогда по формуле ДФП (4.20) имеем

.

Обозначая и , получим

.

В правой части этого равенства первое слагаемое неотрицательно в силу неравенства Коши – Буняковского – Шварца , а второе слагаемое неотрицательно, если . Покажем, что эти слагаемые не могут одновременно обращаться в нуль. Если первое слагаемое равно нулю, то , а, значит, и при . Но тогда по условию . Поэтому . 

Заметим, что условие этого свойства выполняется при условии точного одномерного поиска (3.7) в виде и обеспечении как направления спуска, для которого . Действительно, в силу равенств (4.22) и (4.24) , . Поэтому

.

Свойство сохранения положительной определенности матрицы гарантирует, что направление является направлением спуска.

Свойство 3. При минимизации квадратичной функции с положительно определенной матрицей Гессе методом ДФП с точным одномерным поиском выполняются равенства:

, ; (4.25)

, . (4.26)

Доказательство. Применим метод математической индукции. Из квазиньютоновского условия (4.5) в виде с учетом свойства квадратичной функции (4.4) в виде имеем . Отсюда по формулам (4.24) с точным одномерным поиском получим:

.

Таким образом, равенства (4.25) и (4.26) выполняются при начальных значениях и соответственно.

Предположим, что равенства (4.25) и (4.26) выполнены для некоторого . Докажем, что они выполняются и для . Для с использованием равенств (4.24) получим:

.

Применяя формулу (4.18) для градиента квадратичной функции, имеем

.

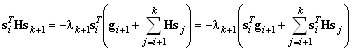По условию точного одномерного поиска (3.7) в виде и сделанного предположения индукции (4.26) получим для условие сопряженности . Это и доказывает справедливость равенств (4.26) для произвольного .

С учетом свойства квадратичной функции (4.4) в виде , предположения индукции (4.25) и доказанного равенства для имеем:

.

Отсюда по формуле ДФП (4.20) получим:

,

То есть по предположениям индукции для . С учетом квазиньютоновского условия (4.5) в виде и свойства квадратичной функции (4.4) в виде имеем . Итак для , что доказывает справедливость равенств (4.25) для произвольного . 

Это свойство показывает, что в силу равенств (4.26) метод ДФП является методом сопряженных направлений, поэтому он минимизирует квадратичную функцию с положительно определенной матрицей Гессе при точном одномерном поиске не более чем за итераций.

Свойство 4. При минимизации квадратичной функции с положительно определенной матрицей Гессе методом ДФП с точным одномерным поиском после итераций .

Доказательство. При сделанных предположениях после итераций метода ДФП в силу выполнения равенств (4.26) при векторы , , …, являются сопряженными. Поэтому по лемме 3.1 они линейно независимы. Представим их столбцами невырожденной матрицы . Поскольку при этом выполняются равенства (4.25) при в виде для , то имеем . Умножая это равенство справа на , придем к равенству , откуда получим . Это означает, что после итераций метода ДФП аппроксимация обратной матрицы Гессе совпадет с ней. 

Свойство 5. При минимизации квадратичной функции с положительно определенной матрицей Гессе методом ДФП с точным одномерным поиском после итераций

. (4.27)

Доказательство. После итераций метода ДФП в силу равенств (4.26) при векторы , , …, являются сопряженными и линейно независимыми. Сформируем из них невырожденную матрицу . Из условий сопряженности (4.26) , где – диагональная матрица с элементами . Поэтому . Тогда , где – диагональная матрица с элементами . Перемножим матрицы в правой части последнего равенства

.

Отсюда с использованием свойства квадратичной функции (4.4) в виде получим равенство (4.27). 

Представим формулу ДФП (4.20) в виде

,

Где

, .

Тогда

.

Для квадратичной функции по свойствам 4 и 5 имеем:

, , .

Отсюда следует, что начальное задание аппроксимирующей матрицы в процессе минимизации квадратичной функции компенсируются последней дробью в формуле (4.20).

Приведенные свойства метода Девидона – Флетчера – Пауэлла проявляются и при минимизации дифференцируемой целевой функции общего вида.

Вычислительные эксперименты, проведенные многими исследователями, показали, что метод Девидона – Флетчера – Пауэлла очень чувствителен к точности одномерного поиска. Если одномерная минимизация целевой функции проводится с невысокой точностью, то эффективность этого метода снижается.

< Предыдущая		Следующая >