34. Метод Девидона-Флетчера–Пауэлла

По аналогии с формулой (4.9) коррекции ранга один рассмотрим формулу коррекции ранга два

, (4.19)

Где используются ненулевые векторы , и скаляры , . Для системы линейных алгебраических уравнений (4.5) получим

.

Раскрывая скобки, после преобразований имеем

,

Где скобки содержат скалярные величины. Это уравнение превратится в тождество, если положить , , , . Тогда равенство (4.19) примет вид

. (4.20)

Эта формула называется Формулой Девидона – Флетчера – Пауэлла (ДФП), а использующий ее квазиньютоновский метод называется Методом Девидона – Флетчера – Пауэлла. Формула (4.14) впервые представлена в 1959 году американским математиком В. Девидоном как часть метода оптимизации, а в 1963 году метод, основанный на формуле (4.20), развит английскими математиками Р. Флетчером и М. Д. Д. Пауэллом. Таким образом, метод ДФП основан на формулах (4.3), (4.7), (4.8) и (4.20). Как и в методе Бройдена первая итерация начинается из заданной начальной точки , и в направлении антиградиента выполняется одномерный поиск:

, , , . (4.21)

Последующие итерации для выполняются по формулам:

, , (4.22)

, , (4.23)

, , . (4.24)

Итерации продолжаются до тех пор, пока выполняется условие

.

По формулам (4.21)–(4.24) составим алгоритм метода ДФП.

Алгоритм метода ДФП.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить и положить , .

2. Вычислить , .

3. Положить , .

4. Вычислить , , .

5. Положить .

6. Вычислить .

7. Если , то перейти к шагу 2.

8. Остановиться.

Пример 4.3. Для вычисления точки минимума квадратичной функции (1.3) с допустимой погрешностью 10–3 метод Девидона – Флетчера – Пауэлла затратил 3 итерации и 19 вычислений функции. При этом траектория минимизации квадратичной функции методом ДФП такая же, как и траектория минимизации этой же функции методом Бройдена из примера 4.1, представленная на рис. 4.1.

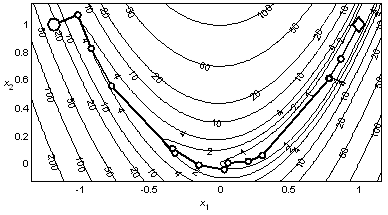
Пример 4.4. На рис. 4.3 представлена траектория минимизации функции Розенброка методом Девидона – Флетчера – Пауэлла. Одномерный поиск с начальным единичным шагом производился комбинацией метода Свенна и метода квадратичной интерполяции с тремя точками при допустимой погрешности шага 10–5. Для нахождения точки минимума с допустимой погрешностью 10–3 метод ДФП использовал 17 итераций и 265 вычислений функции. Траектория минимизации такая же, как и траектория метода Бройдена из примера 4.2, представленная на рис. 4.2.

Рис. 4.3. Минимизация функции Розенброка методом ДФП

< Предыдущая		Следующая >