33. Свойства метода Бройдена

Рассмотрим и обоснуем свойства метода Бройдена.

Свойство 1. Если в формуле Бройдена (4.10) матрица симметрическая, то матрица также симметрическая.

Доказательство. Пусть матрица симметрическая, то есть . Тогда по формуле Бройдена (4.10) с обозначениями и придем к формуле (4.9). Применяя свойства матриц, получим:

.

Следовательно, . 

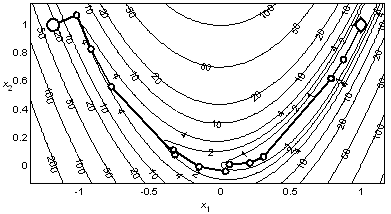
Рис. 4.2. Минимизация функции Розенброка методом Бройдена

Свойство 2. Если в формуле Бройдена (4.10) матрица положительно определенная и , то матрица также положительно определенная.

Доказательство. Пусть матрица положительно определенная, то есть . Тогда по формуле Бройдена (4.10) с обозначениями и получим:

.

При в правой части этого равенства первое слагаемое положительно, а второе неотрицательно, если , то есть если . Тогда . 

Свойство 3. При минимизации квадратичной функции с положительно определенной матрицей Гессе методом Бройдена выполняются равенства:

, . (4.15)

Доказательство. Применим метод математической индукции. При равенство (4.15) вытекает из квазиньютоновского условия (4.5) в виде . Предположим, что равенства (4.15) выполнены для некоторого . Тогда для с учетом свойства квадратичной функции (4.4) в виде получим:

.

Отсюда по формуле Бройдена (4.10) и гипотезе индукции имеем:

, .

С учетом квазиньютоновского условия (4.5) окончательно получим: , . 

Свойство 4. Если при минимизации квадратичной функции с положительно определенной матрицей Гессе метод Бройдена производит линейно независимые направления , , …, , то и минимум находится не более чем за итерацию.

Доказательство. При сделанных предположениях после итераций метода Бройдена выполняются равенства (4.15) при в виде , . Отсюда с учетом свойства квадратичной функции (4.4) в виде имеем: , . Поскольку векторы образуют линейно независимых направлений, которые можно представить столбцами невырожденной матрицы , то справедливо матричное уравнение . Умножая это равенство справа на матрицу , получим , откуда . Поэтому следующая итерация метода Бройдена является итерацией метода Ньютона и приведет к точке минимума квадратичной функции. 

Заметим, что в доказательстве этого свойства не используется условие точного одномерного поиска.

Свойство 5. Если при минимизации квадратичной функции с положительно определенной матрицей Гессе методом Бройдена выполняется точный одномерный поиск, то направления поиска , , …, являются -сопряженными.

Доказательство. При выполнении условий данного утверждения требуется доказать, что

, . (4.16)

Докажем это свойство методом математической индукции. При с учетом (4.14) имеем:

.

Отсюда по свойству 3 в виде и по условию точного одномерного поиска (3.7) в виде получим:

.

Предположим, что равенства (4.16) выполнены для некоторого . Докажем, что они выполняются и для . Для имеем:

.

По свойству 3 получим

, . (4.17)

Очевидно, что

.

С учетом обозначений (4.3) имеем:

.

По свойству квадратичной функции (4.4) в виде получим

. (4.18)

Равенство (4.17) примет вид

.

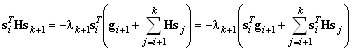По условию точного одномерного поиска (3.7) в виде и сделанного предположения индукции (4.16) окончательно получим для условие сопряженности . Следовательно, равенства (4.16) выполняются для всех . 

Это свойство показывает, что метод Бройдена является методом сопряженных направлений, поэтому он минимизирует квадратичную функцию с положительно определенной матрицей Гессе при выполнении точного одномерного поиска не более чем за итераций.

В случае, когда целевая функция не является квадратичной, применение уравнения (4.10) может привести к нежелательным явлениям. Во-первых, матрица может перестать быть положительно определенной. Во-вторых, поправка может стать неограниченной. В-третьих, если направление случайно совпадет с направлением предыдущей итерации, матрица становится вырожденной или неопределенной. В алгоритме Бройдена это тоже будет иметь место, если либо , либо . Тогда знаменатель формулы (4.10) обращается в нуль. Эта особенность снижает надежность метода Бройдена.

< Предыдущая		Следующая >