36. Метод Бройдена-Флетчера-Гольдфарба-Шанно

Пусть – аппроксимация матрицы Гессе в точке , причем она связана с аппроксимацией обратной матрицы Гессе равенством . Умножая квазиньютоновское условие (4.5) слева на матрицу , после преобразований получим

. (4.28)

Эта формула отличается от формулы (4.5) тем, что матрица заменена матрицей , а векторы и поменялись местами. Выполним те же изменения в формуле ДФП (4.20)

. (4.29)

Эта формула называется Формулой Бройдена – Флетчера – Гольдфарба – Шанно (БФГШ), а использующий ее квазиньютоновский метод называется Методом Бройдена – Флетчера – Гольдфарба – Шанно. Метод БФГШ, основанный на формуле (4.29), представлен в 1970 году независимо английскими математиками Ч. Д. Бройденом и Р. Флетчером, американскими математиками Д. Гольдфарбом и Д. Ф. Шанно. Поскольку здесь аппроксимируется матрица Гессе, то направление одномерного поиска необходимо вычислять не по формуле (4.7), а путем решения системы линейных алгебраических уравнений

. (4.30)

Первая итерация начинается из заданной начальной точки , и в направлении антиградиента выполняется одномерный поиск:

, , , . (4.31)

Последующие итерации проводятся с учетом формул (4.29) и (4.30):

, , (4.32)

, , (4.33)

, , . (4.34)

Итерации продолжаются до тех пор, пока выполняется условие

.

По формулам (4.31)–(4.34) составим алгоритм метода Бройдена – Флетчера – Гольдфарба – Шанно.

Алгоритм метода БФГШ.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить и положить , .

2. Вычислить , .

3. Положить , .

4. Вычислить , , .

5. Положить .

6. Решить СЛАУ .

7. Если , то перейти к шагу 2.

8. Остановиться.

Пример 4.5. Для вычисления точки минимума квадратичной функции (1.3) с допустимой погрешностью 10–3 метод БФГШ затратил 3 итерации и 19 вычислений функции. Траектория поиска такая же, как и траектория метода Бройдена из примера 4.1, представленная на рис. 4.1.

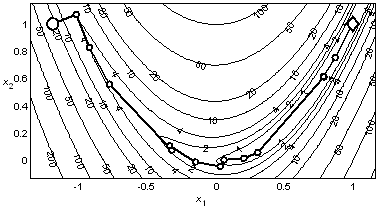
Пример 4.6. На рис. 4.4 показана траектория минимизации функции Розенброка методом БФГШ. Вычисление точки минимума с допустимой погрешностью 10–3 потребовало 17 итераций и 265 вычислений функции, что полностью совпало с результатами метода ДФП из примера 4.4. Траектории поиска на рис. 4.4 и рис. 4.3 также совпадают.

Рис. 4.4. Минимизация функции Розенброка методом БФГШ

Этот метод обладает теми же свойствами, что и метод ДФП, но он менее чувствителен к точности одномерного поиска.

< Предыдущая		Следующая >