26. Метод Флетчера-Ривса
Одним из самых известных методов сопряженных градиентов является Метод Флетчера – Ривса. Приведем описание этого метода для минимизации произвольной целевой функции ![]() .
.
В методе Флетчера – Ривса направления одномерного поиска определяются на основании градиента целевой функции ![]() . Задается начальная точка
. Задается начальная точка ![]() , в ней вычисляется значение градиента
, в ней вычисляется значение градиента ![]() . В направлении антиградиента производится одномерный поиск и находится следующая точка:
. В направлении антиградиента производится одномерный поиск и находится следующая точка:
![]() ,
, ![]() ,
, ![]() . (3.24)
. (3.24)
Последующие итерации основаны на вычислении градиента ![]() , формулах методов спуска (1.16) и методов сопряженных градиентов (3.18):
, формулах методов спуска (1.16) и методов сопряженных градиентов (3.18):
![]() ,
, ![]() ,
, ![]() , (3.25)
, (3.25)
![]() ,
, ![]() . (3.26)
. (3.26)
Итерации продолжаются до тех пор, пока выполняется условие
![]() ,
,
Где ![]() – допустимая погрешность.
– допустимая погрешность.
Вектор ![]() , построенный по формулам (3.25), для квадратичной функции является направлением спуска. Действительно, если
, построенный по формулам (3.25), для квадратичной функции является направлением спуска. Действительно, если ![]() , то с учетом свойств (3.19) получим:
, то с учетом свойств (3.19) получим:
![]() .
.
Заметим, что при ![]() метод Флетчера – Ривса превращается в метод наискорейшего спуска.
метод Флетчера – Ривса превращается в метод наискорейшего спуска.
По формулам (3.24)–(3.26) составим алгоритм метода Флетчера – Ривса.
Алгоритм метода Флетчера – Ривса.
Входные параметры: ![]() – начальная точка поиска,
– начальная точка поиска, ![]() – процедура вычисления функции,
– процедура вычисления функции, ![]() – допустимая погрешность.
– допустимая погрешность.
Выходной параметр ![]() – конечная точка поиска.
– конечная точка поиска.
1. Вычислить ![]() , и положить
, и положить ![]() .
.
2. Вычислить ![]() ,
, ![]() .
.
3. Положить ![]() ,
, ![]() .
.
4. Вычислить ![]() ,
, ![]() .
.
5. Положить ![]() .
.
6. Если ![]() , то перейти к шагу 2.
, то перейти к шагу 2.
7. Остановиться.
Достоинством метода Флетчера – Ривса является то, что его скорость сходимости значительно превышает скорость сходимости метода наискорейшего спуска. Он требует хранения в памяти малого количества информации в виде нескольких ![]() -мерных векторов. Уменьшить объем памяти можно применением модификации предыдущего алгоритма.
-мерных векторов. Уменьшить объем памяти можно применением модификации предыдущего алгоритма.
Алгоритм 2 метода Флетчера – Ривса.
Входные параметры: ![]() – начальная точка поиска,
– начальная точка поиска, ![]() – процедура вычисления функции,
– процедура вычисления функции, ![]() – допустимая погрешность.
– допустимая погрешность.
Выходной параметр ![]() – конечная точка поиска.
– конечная точка поиска.
1. Вычислить ![]() ,
, ![]() и положить
и положить ![]() .
.
2. Вычислить ![]() ,
, ![]() .
.
3. Положить ![]() .
.
4. Вычислить ![]() ,
, ![]() ,
, ![]() .
.
5. Положить ![]() ,
, ![]() .
.
6. Если ![]() , то перейти к шагу 2.
, то перейти к шагу 2.
7. Остановиться.
В отличие от предыдущего алгоритма здесь скалярные произведения градиентов хранятся в скалярных переменных ![]() и
и ![]() , что не требует дополнительного запоминания
, что не требует дополнительного запоминания ![]() -мерного вектора градиента. При решении реальных задач оптимизации значения градиента целевой функции вычисляется по формуле конечной разности вперед, что требует
-мерного вектора градиента. При решении реальных задач оптимизации значения градиента целевой функции вычисляется по формуле конечной разности вперед, что требует ![]() добавочных вычислений функции. Относительно невысокий уровень требований к объему памяти компьютера делает метод Флетчера – Ривса особенно полезным при решении задач оптимизации большой размерности.
добавочных вычислений функции. Относительно невысокий уровень требований к объему памяти компьютера делает метод Флетчера – Ривса особенно полезным при решении задач оптимизации большой размерности.
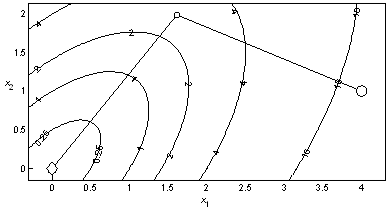
Пример 3.3. На рис. 3.5 представлена траектория минимизации квадратичной функции (1.3) методом Флетчера – Ривса, включающая лучшие точки итераций. Для вычисления точки минимума с допустимой погрешностью 10–3 метод затратил 3 итерации, причем значение функции 1,3∙10–14 найдено за две итерации при погрешности вычисления точки минимума 8,8∙10–8, а последняя итерация использована для проверки критерия окончания вычислений. Значения функции вычислены 19 раз. При этом траектория минимизации квадратичной функции методом Флетчера – Ривса такая же, как и траектория минимизации этой же функции модифицированным методом Ньютона с направлением спуска из примера 2.5, представленная на рис. 2.4.
|
|
|
Рис. 3.5. Минимизация квадратичной функции методом Флетчера-Ривса |
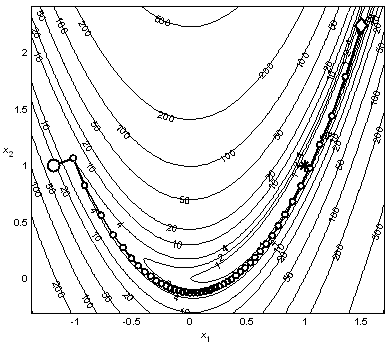
Пример 3.4. На рис. 3.6 представлена траектория поиска минимума функции Розенброка методом Флетчера – Ривса. До уменьшения шага с допустимой погрешностью 10–3 метод затратил 49 итераций и 461 вычисление функции. Метод проскочил мимо точки минимума, отмеченной звездочкой.
Недостатком метода Флетчера – Ривса является то, что он очень чувствителен к точности одномерного поиска, а также подвержен существенному влиянию ошибок машинных вычислений. При минимизации функций общего вида его эффективность может снижаться из-за нарушения условий сопряженности направлений поиска.
При нарушении условий сопряженности направлений метод Флетчера – Ривса начинает вычислять направления, движение вдоль которых неэффективно для минимизации функции. В связи с этим процесс построения сопряженных направлений вида (3.25) целесообразно вести циклами, начиная каждый цикл с направления наискорейшего спуска, то есть с антиградиента: как и в начальной итерации метод, запускается из текущей точки поиска по антиградиенту. Такое обновление работы метода называется повторным стартом или Рестартом. С помощью рестартов эффективность метода Флетчера – Ривса можно существенно повысить. Для этого в приведенных алгоритмах через ![]() или
или ![]() итераций переходят не к шагу 2, а к шагу 1.
итераций переходят не к шагу 2, а к шагу 1.
|
|
|
Рис. 3.6. Минимизация функции Розенброка методом Флетчера-Ривса |
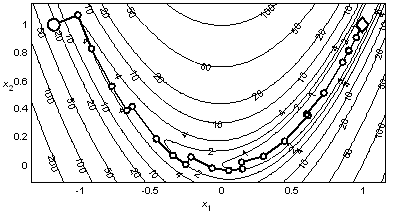
Пример 3.5. На рис. 3.7 представлена траектория минимизации функции Розенброка методом Флетчера – Ривса с рестартами, которые выполняются через каждые ![]() итераций. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 24 итерации и 327 вычислений функции.
итераций. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 24 итерации и 327 вычислений функции.
|
|
|
Рис. 3.7. Минимизация функции Розенброка методом Флетчера – Ривса С рестартами |
| < Предыдущая | Следующая > |
|---|