25. Методы сопряжённых градиентов
В методах сопряженных направлений сопряженные векторы как направления одномерного поиска можно определять разными способами.
Методами сопряженных градиентов для минимизации квадратичной функции ![]() называются методы сопряженных направлений, в которых сопряженные векторы как направления одномерного поиска определяются на основании значений градиента целевой функции
называются методы сопряженных направлений, в которых сопряженные векторы как направления одномерного поиска определяются на основании значений градиента целевой функции ![]() .
.
Рассмотрим общие свойства методов сопряженных градиентов, в которых применяются формулы методов сопряженных направлений (3.13). Справедлива теорема методов сопряженных градиентов, где как и ранее ![]() .
.
|
|
|
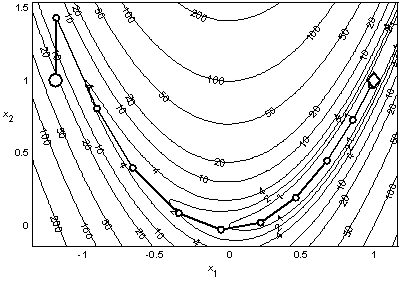
Рис. 3.4. Минимизация функции Розенброка методом Пауэлла |
Теорема 3.3. Метод сопряженных градиентов является методом сопряженных направлений (3.13), в котором векторы направлений вычисляются по формулам
![]() ,
, ![]() ,
, ![]() ,
, ![]() , (3.18)
, (3.18)
И выполняются свойства
![]() ,
, ![]() ;
; ![]() ,
, ![]() . (3.19)
. (3.19)
Доказательство. Пусть в методе сопряженных направлений (3.13) начальное направление поиска определяется по антиградиенту ![]() в начальной точке поиска
в начальной точке поиска ![]() , а последующие направления
, а последующие направления ![]() вычисляются как сумма антиградиента
вычисляются как сумма антиградиента ![]() и линейной комбинации предыдущих направлений поиска:
и линейной комбинации предыдущих направлений поиска:
![]() ,
, ![]() . (3.20)
. (3.20)
При этом коэффициенты ![]() выбирают таким образом, чтобы направления были сопряженными. При таком выборе (3.20) дает:
выбирают таким образом, чтобы направления были сопряженными. При таком выборе (3.20) дает:
 ,
, ![]() .
.
Отсюда с учетом (3.15) получим важное свойство методов сопряженных градиентов:
![]() ,
, ![]() . (3.21)
. (3.21)
Тем самым доказана первая группа равенств (3.19).
Умножим равенство (3.20) скалярно на вектор ![]() :
:
![]() ,
, ![]() .
.
По свойству методов сопряженных направлений (3.15) имеем:
![]() ,
, ![]() . (3.22)
. (3.22)
Тем самым доказана вторая группа равенств (3.19).
Для определения коэффициентов ![]() в равенстве (3.20) умножим их скалярно на вектор
в равенстве (3.20) умножим их скалярно на вектор ![]() при
при ![]() :
:
![]() ,
, ![]() .
.
С использованием определения сопряженности (3.11) получим:
![]() ,
, ![]() .
.
Умножая это равенство на ![]() и учитывая формулу (3.9) в виде
и учитывая формулу (3.9) в виде ![]() , имеем:
, имеем:
![]() ,
, ![]() .
.
Тогда с учетом свойств (3.21) и (3.22) получим:
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
Отсюда
![]() ,
, ![]() ;
; ![]() .
.
Обозначая ![]() , для формулы направления (3.20) окончательно имеем:
, для формулы направления (3.20) окончательно имеем:
![]() ,
, ![]() ,
, ![]() . (3.23)
. (3.23)
Равенства (3.18) доказаны. Тем самым доказана теорема 3.3.
Для обеспечения сопряженности векторов направлений в методе сопряженных градиентов достаточно учитывать только предыдущий вектор направления. Формула для вычисления ![]() в равенствах (3.23) представлена английскими математиками Р. Флетчером и К. М. Ривсом в 1964 году и называется Формулой Флетчера – Ривса. Метод сопряженных градиентов обладает всеми свойствами методов сопряженных направлений и минимизирует квадратичную функцию при точном одномерном поиске не более чем за
в равенствах (3.23) представлена английскими математиками Р. Флетчером и К. М. Ривсом в 1964 году и называется Формулой Флетчера – Ривса. Метод сопряженных градиентов обладает всеми свойствами методов сопряженных направлений и минимизирует квадратичную функцию при точном одномерном поиске не более чем за ![]() итераций.
итераций.
Важной особенностью формул (3.23) является то, что для построения вектора направления ![]() нужны лишь градиенты
нужны лишь градиенты ![]() и
и ![]() в текущей и предыдущей точках соответственно, а также предыдущий вектор направления
в текущей и предыдущей точках соответственно, а также предыдущий вектор направления ![]() . Это обстоятельство оказывается особенно полезным для применения метода к гладким функциям общего вида.
. Это обстоятельство оказывается особенно полезным для применения метода к гладким функциям общего вида.
| < Предыдущая | Следующая > |
|---|