27. Метод Полака–Рибьера

Этот метод сопряженных градиентов представлен американскими математиками Э. Полаком и Д. Рибьером в 1969 году. Для его обоснования применим первое из свойств (3.19) в виде , . Из этой формулы следует, что

.

Поэтому формулу Флетчера – Ривса (3.23) для вычисления коэффициента можно представить в виде:

, . (3.27)

Эта формула называется Формулой Полака – Рибьера, а онованный на ее использовании метод называется Методом Полака – Рибьера. В этом методе задается начальная точка , в ней вычисляется значение градиента . В направлении антиградиента производится одномерный поиск и находится следующая точка:

, , . (3.28)

Последующие итерации основаны на вычислении градиента , формулах методов спуска (1.16), методов сопряженных градиентов (3.18) и формулы Полака – Рибьера (3.27):

, , , (3.29)

, . (3.30)

Итерации продолжаются до тех пор, пока выполняется условие

,

Где – допустимая погрешность. Формулы метода Полака – Рибьера (3.28)–(3.30) отличаются от соответствующих формул метода Флетчера – Ривса (3.24)–(3.26) только формулой вычисления коэффициента . По формулам (3.28)–(3.30) составим алгоритм метода Полака – Рибьера.

Алгоритм метода Полака – Рибьера.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить и положить .

2. Вычислить , .

3. Положить , .

4. Вычислить , .

5. Положить .

6. Если , то перейти к шагу 2.

7. Остановиться.

Этот алгоритм отличается от алгоритма метода Флетчера – Ривса только вычислением параметра на шаге 4.

Пример 3.6. Для вычисления точки минимума квадратичной функции (1.3) с допустимой погрешностью 10–3 метод Полака – Рибьера затратил 3 итерации 19 вычислений функции, причем за две итерации найдено значение функции 1,8∙10–14. При этом траектория минимизации такая же, как и на рис. 3.5 для метода Флетчера – Ривса.

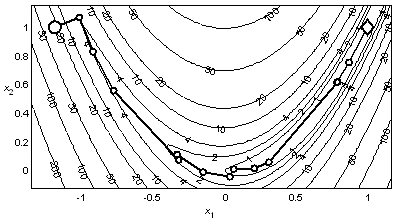
Пример 3.7. На рис. 3.8 представлена траектория минимизации функции Розенброка методом Полака – Рибьера. Вычисление точки минимума с допустимой погрешностью 10–3 потребовало 17 итераций и 266 вычислений функции.

Рис. 3.8. Минимизация функции Розенброка методом Полака – Рибьера

Если все вычисления, включая одномерный поиск, проводятся с абсолютной точностью, то при минимизации квадратичной положительно определенной целевой функции методы Флетчера – Ривса и Полака – Рибьера производят одинаковые последовательности точек поиска, то есть траектории поиска в обоих методах совпадают.

Однако при минимизации целевых функций общего вида в результате большого количества вычислительных экспериментов установлено, что метод Полака – Рибьера гораздо эффективнее метода Флетчера – Ривса. Эвристическое объяснение этого факта состоит в том, что в связи с отличием целевой функции от квадратичной функции и неточностью одномерного поиска вырабатываемые методом Полака – Рибьера направления все с меньшей точностью удовлетворяют условиям сопряженности. В результате вновь построенный по формуле (3.29) вектор направления становится почти ортогональным градиенту и метод может временно «застревать». В таком случае имеем , поэтому по формуле Полака – Рибьера (3.27) получим значение , близкое к нулю. Но тогда следующий вектор направления , построенный согласно (3.29), оказывается близким к , и автоматически происходит рестарт метода. Формула Флетчера – Ривса (3.23) таким свойством не обладает, поэтому в методе Флетчера – Ривса применяют принудительные рестарты. Метод Полака – Рибьера также может применяться с рестартами.

Итак, метод Полака – Рибьера эффективен даже при наличии ошибок вычислений и обладает малой чувствительностью к ошибкам округления при проведении одномерных поисков. Ему принадлежит ведущая роль при решении задач безусловной минимизации большой размерности.

В настоящее время построено и применяется много других вариантов методов сопряженных градиентов. В частности, кроме формулы (3.27) известны формулы Хестенса – Штифеля, Диксона и Даи – Юана:

, , .

Все эти формулы производят одинаковые направления поиска, когда используются для минимизации квадратичной функции с положительно определенной матрицей Гессе и точным одномерным поиском. Однако для нелинейной функции общего вида с неточным одномерным поиском их действия значительно отличаются.

< Предыдущая		Следующая >