17. Вычисление матрицы Гессе

Для минимизации дважды дифференцируемой целевой функции , зависящей от переменных , , …, , все варианты метода Ньютона, которые являются методами второго порядка, используют матрицу Гессе вторых частных производных

.

По теореме Шварца

, , .

Поэтому матрица Гессе является симметрической матрицей, для которой симметричные относительно главной диагонали элементы совпадают: . В силу этого свойства при транспонировании матрица Гессе не изменяется .

Во многих задачах оптимизации, которые встречаются на практике, целевые функции представляются сложными выражениями или вычисляются алгоритмически, поэтому матрица Гессе в методах второго порядка определяется численно с помощью конечных разностей.

Для вычисления матрицы Гессе целевую функцию разложим в ряд Тейлора, учитывая слагаемые второго порядка малости:

.

Вначале рассмотрим квадратичную функцию двух переменных при :

. (2.13)

Для такой функции

, .

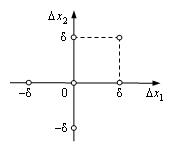
Рис. 2.10. Точки для вычислений

В силу симметричности матрицы Гессе . Поэтому функция (2.13) имеет шесть неизвестных параметров: , , , , , . Эти параметры вычислим по шести значениям функции в различных ее точках (рис. 2.10). Положим , зададим точки , , , , , и вычислим значения функции в этих точках: , , , , , . Подставляя эти значения в уравнение (2.13), получим систему шести уравнений с шестью неизвестными, решая которую имеем:

, , ,

, ,

.

Полученные для квадратичной функции (2.13) формулы обобщаются для вычисления градиента и матрицы Гессе произвольной функции переменных с использованием ортов системы координат , .

Проекции градиента вычислим по формуле центральных разностей (1.22):

, . (2.14)

Диагональные элементы матрицы Гессе вычисляются по формуле конечной разности второго порядка:

, . (2.15)

Недиагональные элементы матрицы Гессе вычислим по формуле

, (2.16)

Где , .

Формулы (2.14)–(2.16) кроме значения целевой функции в точке требуют дополнительных вычислений значений функции. При этом точность вычисления градиента и матрицы Гессе существенно зависит от величины приращения аргумента , которую связывают со значением машинного эпсилон . Обычно полагают . По формулам (2.14)–(2.16) составлен алгоритм вычисления градиента и матрицы Гессе для функции многих переменных.

Алгоритм вычисления градиента и матрицы Гессе.

Входные параметры: и – точка, в которой вычисляется градиент, и значение в ней функции; – процедура вычисления целевой функции; – параметр приращения аргумента.

Выходные параметры: – градиент, – матрица Гессе.

1. Положить , , , , , .

2. Вычислить , , , .

3. Вычислить , .

4. Положить , , .

5. Если , то положить и перейти к шагу 2.

6. Положить .

7. Положить , .

8. Вычислить , , .

9. Положить , .

10. Если , то положить и перейти к шагу 8.

11. Положить .

12. Если , то положить и перейти к шагу 7.

13. Остановиться.

В этом алгоритме на шагах 2–5 вычисляются градиент и диагональные элементы матрицы Гессе, а на шагах 6–12 вычисляются недиагональные элементы матрицы Гессе. В примерах 2.1–2.10 градиент и матрица Гессе вычислены по приведенному алгоритму со значением параметра .

< Предыдущая		Следующая >