16. Метод Марквардта

Этот метод является комбинацией методов наискорейшего спуска и Ньютона. Выше было отмечено, что движение в направлении антиградиента из начальной точки поиска , расположенной на значительном расстоянии от точки минимума , обычно приводит к существенному уменьшению целевой функции. С другой стороны, направления эффективного поиска в окрестности точки минимума определяются по методу Ньютона.

Идея объединения методов наискорейшего спуска и Ньютона представлена американским математиком Д. Марквардтом в 1963 г. Он вместо формулы метода Ньютона (2.1) использовал формулу

, (2.9)

Где – скалярный параметр, – единичная матрица той же размерности, что и . При большом значении матрицей в левой части уравнения (2.9) можно пренебречь, тогда получим уравнение . В этом случае направление вектора совпадает с антиградиентом, то есть направлением наискорейшего спуска. Если же , то в уравнении (2.9) можно пренебречь слагаемым . Тогда (2.9) превращается в (2.1) и становится шагом метода Ньютона. При промежуточном значении направление вектора , удовлетворяющего (2.9), лежит между направлением антиградиента и направлением метода Ньютона. На этом свойстве уравнения (2.9) и основан метод Марквардта.

Начальное значение выбирается достаточно большим, , а затем в процессе поиска уменьшается посредством умножения на коэффициент . Таким образом, на начальных этапах выполняются шаги метода наискорейшего спуска , а на конечных этапах используется шаг метода Ньютона. Формулы метода Марквардта можно представить в виде:

, , . (2.10)

Итерации продолжаются до тех пор, пока выполняется условие

Где – допустимая погрешность. Параметр метода Марквардта позволяет не только изменять направление поиска, но и регулировать длину шага. Если шаг слишком большой и , то полагают и опять применяют формулы (2.10) уже с меньшим шагом .

Формула Марквардта (2.9) позволяет устранить ещё один недостаток метода Ньютона, который связан с возможной плохой обусловленностью СЛАУ (2.1). Плохо обусловленной называется система уравнений, в которой малые погрешности исходных данных вызывают большие погрешности решения. Числом обусловленности матрицы называется произведение норм этой и обратной к ней матриц

Для единичной матрицы число обусловленности , а для произвольной матрицы . Чем больше число обусловленности матрицы, тем хуже обусловлена соответствующая СЛАУ. В частности, матрица может быть вырожденной, и тогда СЛАУ (2.1) не имеет решения в отличие от системы (2.9).

В точках поиска, далёких от минимума, матрица Гессе является, как правило, плохо обусловленной матрицей, но в этих точках для метода Марквардта , поэтому , а, значит,

Поэтому в методе Марквардта СЛАУ (2.9), определяющая направления поиска, хорошо обусловлена. Кроме того, поскольку единичная матрица положительно определена, то это свойство выполняется и для матрицы СЛАУ (2.9), так что найденное путем решения этой системы направление является направлением спуска.

По формулам (2.10) составим алгоритм метода Марквардта.

Алгоритм метода Марквардта.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, и – параметры метода, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить .

2. Вычислить , и положить .

3. Решить СЛАУ .

4. Вычислить , .

5. Если , то положить и перейти к шагу 3.

6. Положить , , .

7. Если , то перейти к шагу 2.

8. Остановиться.

В этом алгоритме можно положить , . Алгоритм метода Марквардта характеризуется относительной простотой, свойством убывания значений целевой функции при переходе от итерации к итерации, высокой скоростью сходимости в окрестности точки минимума , а также отсутствием процедуры одномерного поиска.

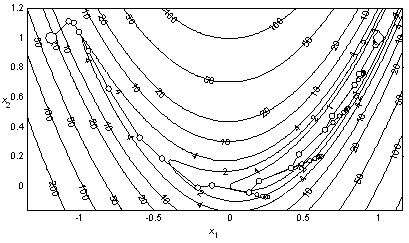
Пример 2.7. На рис. 2.6 показана траектория минимизации квадратичной функции (1.3) методом Марквардта со всеми точками поиска. Для нахождения точки минимума с допустимой погрешностью 10–3 метод использовал 13 итераций и 79 вычислений функции.

Рис. 2.6. Минимизация квадратичной функции методом Марквардта

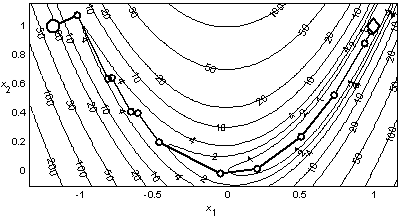
Пример 2.8. На рис. 2.7 представлена траектория поиска минимума функции Розенброка методом Марквардта со всеми точками поиска. Для нахождения точки минимума с допустимой погрешностью 10–3 метод использовал 21 итерацию и 151 вычисление функции.

Рис. 2.7. Минимизация функции Розенброка методом Марквардта

В некоторых случаях применение одномерного поиска позволяет повысить надежность метода Марквардта. В методе Марквардта с одномерным поиском применяются формулы:

, , (2.11)

, . (2.12)

Итерации продолжаются до тех пор, пока выполняется условие

Где – допустимая погрешность. По формулам (2.11) и (2.12) составим алгоритм метода Марквардта с одномерным поиском.

Алгоритм метода Марквардта с одномерным поиском.

Выходной параметр – конечная точка поиска.

1. Вычислить , .

2. Решить СЛАУ .

3. Вычислить , .

4. Положить , .

5. Если , то перейти к шагу 1.

6. Остановиться.

В этом алгоритме можно положить , .

Пример 2.9. На рис. 2.8 представлена траектория поиска минимума квадратичной функции (1.3) методом Марквардта с одномерным поиском. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 11 итераций и 101 вычисление функции. Сравнивая результаты этого примера с результатами примера 1.7 для метода наискорейшего спуска, отметим уменьшение числа итераций за счет более эффективного направления поиска на завершающих итерациях из-за увеличения количества вычислений функции, связанного с нахождением матрицы Гессе. Траектории поиска на рис. 1.7 и рис. 2.8 выглядят одинаково, так как на начальных итерациях метода Марквардта преобладает направление наискорейшего спуска. Для квадратичных функций метод Маркварда использовать нецелесообразно.

Пример 2.10. На рис. 2.9 представлена траектория поиска минимума функции Розенброка методом Марквардта с одномерным поиском. Для нахождения точки минимума с допустимой погрешностью 10–3 метод использовал 15 итераций и 398 вычислений функции. Здесь количество вычислений функции также оказалось больше, чем для всех предыдущих вариантов метода Ньютона.

Рис. 2.8. Минимизация квадратичной функции методом Марквардта

С одномерным поиском

Рис. 2.9. Минимизация функции Розенброка методом Марквардта

С одномерным поиском

Метод Марквардта широко используется при решении задач, в которых целевая функция записывается в виде суммы квадратов. Именно такая задача и рассматривалась Марквардтом. Метод Марквардта также называется Методом Левенберга – Марквардта.

< Предыдущая		Следующая >