15. Метод Ньютона с направлением спуска

Для повышения эффективности метода Ньютона необходимо обеспечить такое направление одномерного поиска, которое гарантированно приводит к убыванию функции, то есть является направлением спуска. Два распространенных случая, в которых метод Ньютона приводит к ошибочным направлениям, связаны с точками максимума целевой функции и седловыми точками. В этих и других случаях необходимо проверять, является ли направление метода Ньютона направлением спуска. Если – направление спуска, то для него , то есть скалярное произведение вектора направления из точки и вектора градиента в этой точке отрицательно. В геометрическом смысле это означает, что векторы и образуют тупой угол . Действительно, если , то из неравенства следует , то есть .

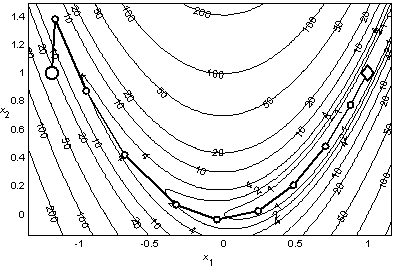
Рис. 2.3. Минимизация функции Розенброка методом Ньютона С одномерным поиском

Если условие не выполняется, то вектор не является направлением спуска. В этом случае для задания направления спуска целесообразно использовать антиградиент . Таким образом, направление спуска в модифицированном методе Ньютона можно задать формулами:

; (2.6)

Вычислительные эксперименты показывают, что для функции общего вида наибольшее уменьшение значений функции на первой итерации обеспечивается в направлении наискорейшего спуска. Поэтому первую итерацию модифицированного метода Ньютона из заданной начальной точки целесообразно проводить в направлении антиградиента с использованием одномерного поиска:

, , . (2.7)

Последующие итерации проводятся по формулам:

, , (2.8)

Где направление поиска определяется формулой (2.6). Итерации продолжаются до тех пор, пока выполняется условие

,

Где – допустимая погрешность, . По формулам (2.6)–(2.8) составим алгоритм метода Ньютона с направлением спуска.

Алгоритм метода Ньютона с направлением спуска.

Входные параметры: – начальная точка поиска, – процедура вычисления функции, – допустимая погрешность.

Выходной параметр – конечная точка поиска.

1. Вычислить .

2. Вычислить , .

3. Положить .

4. Вычислить , .

5. Решить СЛАУ .

6. Если , то положить , иначе положить .

7. Вычислить , .

8. Положить .

9. Если , то перейти к шагу 4.

10. Остановиться.

По сравнению с предыдущим алгоритмом метода Ньютона в этом алгоритме добавлены шаги 1–3, на которых выполняется начальный одномерный поиск в направлении антиградиента, и шаг 6, на котором задается направление спуска.

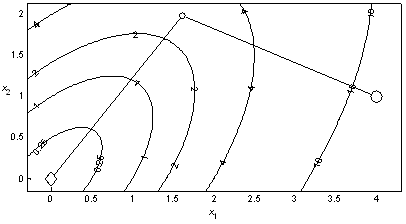
Пример 2.5. На рис. 2.4 показана траектория минимизации квадратичной функции (1.3) модифицированным методом Ньютона с направлением спуска. Для нахождения точки минимума с допустимой погрешностью 10–3 метод использовал 3 итерации и выполнил 26 вычислений функции.

Рис. 2.4. Минимизация квадратичной функции методом Ньютона С направлением спуска

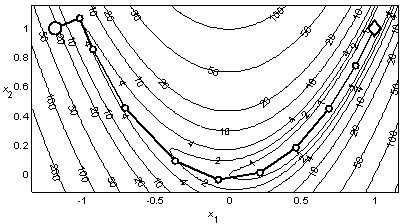
Пример 2.6. На рис. 2.5 представлена траектория поиска минимума функции Розенброка методом Ньютона с направлением спуска. Для нахождения точки минимума с допустимой погрешностью 10–3 метод затратил 12 итераций и 307 вычислений функции.

Рис. 2.5. Минимизация функции Розенброка методом Ньютона С направлением спуска

Метод Ньютона с одномерным поиском и заданием направления спуска надежнее предыдущих вариантов метода Ньютона.

< Предыдущая		Следующая >