0. Содержание

1. Числовые ряды. Критерий Коши сходимости. Свойства сходящихся рядов.

2. Ряды с неотрицательными членами. Теоремы сравнения. Признаки Даламбера, Коши, Гаусса.

3. Интегральный признак сходимости. Сходимость ряда .

4. Абсолютная сходимость. Свойства абсолютно сходящихся рядов.

5. Условная сходимость. Теорема Лейбница.

6. Равномерная сходимость функциональной последовательности, ряда. Признак Вейерштрасса.

7. Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование ряда.

8. Степенные ряды. Радиус сходимости. Непрерывность суммы. Почленное интегрирование и дифференцирование.

9. Разложение элементарных функций в степенные ряды.

10. Ортонормированные системы функций. Обобщенные ряды Фурье. Тригонометрические ряды Фурье. Теорема сходимости.

11. Дифференциальные уравнения 1-го порядка. Уравнение . Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида .

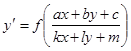12. Линейное дифференциальное уравнение 1-го порядка.

13. Дифференциальное уравнение N-ного порядка. Задача Коши для уравнения . Понижение порядка дифференциального уравнения.

14. Линейное дифференциальное уравнение N-ного порядка. Свойства линейного однородного дифференциального уравнения.

15. Линейная зависимость функций. Определитель Вронского.

16. Фундаментальная система решений линейного однородного уравнения.

17. Линейное неоднородное уравнение. Принцип суперпозиции.

18. Метод вариации постоянных.

19. Линейное однородное дифференциальное уравнение с постоянными коэффициентами. Характеристическое уравнение. Общее решение.

20. Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами.

Следующая >