18. Метод вариации постоянных

Вернемся к неоднородному уравнению (1). Предположим, что мы можем найти фундаментальную систему решений уравнения (2). Тогда, по теореме 9 (Билет 16), любое решение этого уравнения имеет вид: (12). Предположим также, что нам удалось найти некоторое решение уравнения (1). По теореме 3, любое решение этого уравнения имеет вид: , согласно (12). Итак, для нахождения всех решений уравнения (1) требуется найти какое-то одно его решение . Для этого можно использовать Метод вариации постоянных, который состоит в том, что решение уравнения (1) ищется в виде (13), где - фундаментальная система решений уравнения (2). Отметим, что (13) напоминает (12), но имеет существенное отличие от этого равенства состоящее в том, что в (12) все - постоянные, а в (13) это – неизвестные функции от . Потребуем, чтобы кроме равенства (13) выполнялись такие равенства: 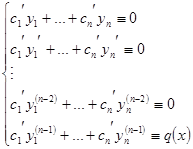(14). Из (13) и (14) следует, что ; и т. д., и, наконец, . Поэтому подстановка в левую часть уравнения (1) дает , т. е. обращает уравнение в верное равенство. Поэтому , определяемое равенством (13) и системой условий (14) является решением уравнения (1). По теореме 1 это решение – единственное.

Для того, чтобы отыскать следует воспользоваться системой (14), рассматривая ее как систему линейных уравнений относительно неизвестных с определителем . Решая систему, находим а затем, интегрированием, находим .

< Предыдущая		Следующая >