16. Степенные ряды
Степенным Рядом называется функциональный ряд вида:

Где множители при степенях (X–X0) – Коэффициенты ряда, число X0 – центр интервала сходимости. При частном значении переменной X степенной ряд становится числовым. Сходимость степенного ряда зависит от величины X. Из теоремы Абеля для степенных рядов следует, что область сходимости всякого степенного ряда – некоторый интервал (X0–R, X0+R), называемый Интервалом сходимости. Во всех точках этого интервала степенной ряд сходится и притом абсолютно, вне интервала – ряд расходится. На границе интервала различные степенные ряды ведут себя по-разному. Число R – половина длины интервала сходимости – Радиус сходимости. Если степенной ряд сходится лишь в одной точке, то радиус R = 0. Если ряд сходится при любом X, То R = ¥. Радиус сходимости степенного ряда можно найти по формуле:

Если соответствующие пределы существуют – конечные или бесконечные. При этом R = 0, если L = 0 и R = ¥, если L = 0.
Пример 8. Найти область сходимости степенного ряда
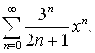
Решение. В развернутом виде ряд выглядит следующим образом

Коэффициенты ряда:

Найдем радиус сходимости

Заключаем, что интервал сходимости (-1/3, 1/3).
Исследуем далее сходимость степенного ряда в граничных точках интервала:
а) при X=1/3 получим числовой положительный ряд:
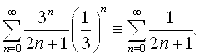
Этот ряд расходится, что видно из сравнения его с гармоническим рядом.
б) при X= -1/3 получим знакочередующийся ряд:

Члены этого ряда удовлетворяют условиям теоремы Лейбница:

Знакочередующийся ряд сходится, т. е. при X = -1/3 степенной ряд сходится и окончательно область сходимости степенного ряда определяется неравенствами –1/3 £ X < 1/3.
При решении примеров на применение степенных разложений к приближенным вычислениям следует использовать известные формулы разложения элементарных функций в ряды Маклорена. Они помещены в таблице 2. Заметим, что важную роль здесь выполняет следствие из теоремы Лейбница: для сходящегося знакочередующегося ряда остаток по абсолютной величине не превосходит первого из отброшенных членов. Опираясь на это следствие легко установить, сколько членов ряда нужно просуммировать, чтобы получить результат с заданной точностью. Разумеется, все расчеты надо проводить в рамках этой точности.
Пример 9. С точностью до e = 0.0001 вычислить Exp(-0.1).
Решение. Используем разложение (табл. 2)

Полагая X= -0.1, имеем
![]()
Получили знакочередующийся ряд. Величина его остатка по абсолютной величине не превосходит первого из отброшенных членов. Возьмем 4 члена ряда, тогда погрешность не превышает величины 0.0000042, т. е.
![]()
Каждое из оставленных четырех слагаемых учитываем, удерживая 5 цифр после запятой. При этом, округляя, в ответе будем иметь 4 верных десятичных знака: Exp(-0.1)= 0.9048.
Пример 10. С точностью до E = 0.0001 вычислить интеграл
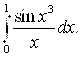
Решение. Интеграл вычислим, разлагая подынтегральную функцию в степенной ряд. При этом воспользуемся формулой (табл. 2):

Имеем

Степенной ряд можно почленно интегрировать и почленно дифференцировать любое число раз, при этом радиус сходимости не меняется (Основное свойство степенных рядов). Выполняя почленное интегрирование, имеем

Получился знакочередующийся ряд, причем ![]() Поэтому с заданной точностью имеем
Поэтому с заданной точностью имеем
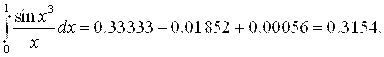
| < Предыдущая | Следующая > |
|---|