15. Знакочередующиеся ряды

Ряд, составленный из положительных и отрицательных членов (знакопеременный ряд) называется Абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из модулей его членов, расходится, тогда знакопеременный ряд называется Условно (неабсолютно) Сходящимся.

Рассмотрим далее числовые ряды, любые два соседние члены которых имеют противоположные знаки (Знакочередующиеся ряды):

Исследование сходимости знакочередующихся рядов можно начинать с проверки абсолютной сходимости. Если ряд, составленный из абсолютных величин, сходится, то и сам знакопеременный ряд сходится. Если же окажется, что данный знакочередующийся ряд не обладает абсолютной сходимостью, то исследование продолжают с помощью признака Лейбница:

Теорема Лейбница. Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю при n ®¥ , то ряд сходится. Его сумма имеет знак первого члена, абсолютное значение этой суммы не превышает абсолютное значение первого из членов ряда:

Важное для практики значение имеет Следствие Из теоремы Лейбница: для сходящегося знакочередующегося ряда абсолютная ошибка приближенного равенства (абсолютная величина остатка ряда) не превосходит модуль Первого Из Отброшенных членов: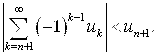

Пример 7. Исследовать сходимость ряда

Решение. Данный ряд знакочередующийся, т. к.

Исходный ряд можно переписать в виде

Рассмотрим сначала ряд, составленный из абсолютных величин исходного ряда:

Сравним его с гармоническим рядом 1+1/2+1/3+…+1/N+…, о котором известно, что он расходится. Так как

То по второму признаку сравнения заключаем, что ряд из модулей расходится и, следовательно, исходный ряд абсолютно не сходится. Продолжим исследование с помощью признака Лейбница: члены исходного ряда удовлетворяют условиям : во-первых, монотонного убывания абсолютных величин членов ряда, во-вторых, общий член ряда стремится к нулю. В самом деле, в промежутке [0, p/2] функция Y = tg X Монотонно возрастает, а при N = 1, 2, … выполняются неравенства, а также необходимое условие:

Окончательно заключаем, исходный ряд сходится Условно.

< Предыдущая		Следующая >