14. Положительные ряды

Для исследования сходимости Положительных рядов (т. е. рядов с неотрицательными членами: ³0) применяют достаточные признаки сходимости рядов. Среди них наиболее часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши (Табл. 1).

Пример 2. Исследовать сходимость ряда

Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд

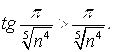
Показатель степени гармонического ряда P=4/5<1, поэтому «эталонный» ряд расходящийся. Члены исходного ряда для всех n³3 превосходят соответствующие члены «эталонного» ряда:

Применяя первый признак сравнения, получаем, поскольку расходится «меньший» эталонный ряд, то расходится и «больший» исходный ряд.

Пример 3. Исследовать сходимость ряда

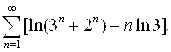
Решение. Преобразуем общий член исходного ряда

Исходный ряд сравним с “эталонным” рядом

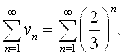
Это “геометрический ряд, он сходится, т. к. знаменатель прогрессии Q=2/3<1. Поскольку

- конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится.

Пример 4. Исследовать сходимость ряда

Решение. Применим признак Даламбера. Записываем N-Ый член ряда:

(n+1)-Ый член получим, если в выражении везде N заменим на (n+1):

Найдем предел отношения:

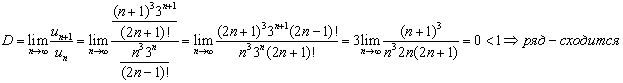
Пример 5. Исследовать сходимость ряда

Решение. Здесь удобно применить радикальный признак Коши:

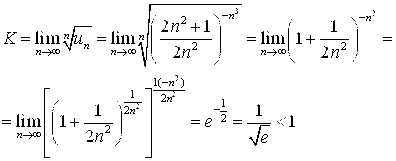
Следовательно, ряд сходится. Подчеркнем, здесь использовали известный « второй замечательный» предел.

Пример 6. Исследовать сходимость ряда

Решение. Рассмотрим функцию

Она при x³2 положительная, непрерывная и монотонно убывает. (Заметим, что эта функция получается из выражения общего члена ряда при замене N На X). Можно применять интегральный признак. Исследуем сходимость несобственного интеграла:

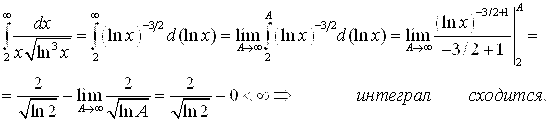
Из интегрального признака заключаем, поскольку несобственный интеграл сходится, то сходится и исследуемый ряд.

< Предыдущая		Следующая >