13. Элементы теории рядов. Понятие числового ряда. Необходимый признак сходимости

Определение. Числовой ряд (Бесконечная сумма) – это пара последовательностей чисел и , таких, что .

Числовой ряд обозначают символом

.

Здесь (n=1, 2, … ) – n-ый член ряда, а сумма конечного числа n первых членов ряда называется n-ой Частичной Суммой ряда.

Если существует конечный предел последовательности Частичных сумм ,

То этот предел называется суммой ряда, а сам ряд называется Сходящимся. Если конечный предел частичных сумм не существует, то ряд называется Расходящимся.

Необходимый признак сходимости ряда: если ряд сходится, то общий член ряда стремится к нулю: . Ряд может сходиться лишь в том случае, когда его общий член При n®¥ является бесконечно малой величиной.

Если необходимое условие сходимости ряда не выполнено: , либо предел не

существует, то ряд расходится (Достаточный признак расходимости рядов).

Пример 1. Найти общий член ряда

Доказать, что этот ряд расходится.

Решение. Последовательно рассмотрим члены ряда:

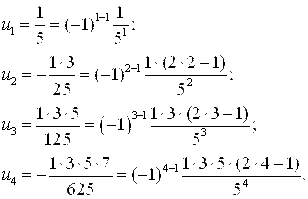
Подмечая закономерность, можно видеть, что общий член ряда выражается формулой

Представим общий член ряда в виде

Ясно, что при n³4 || > 3/25, поскольку все сомножители - дроби, кроме первых трех, больше 1.

Отсюда следует , необходимое условие сходимости не выполнено, ряд расходится.

< Предыдущая		Следующая >