12. Линейные неоднородные дифференциальные уравнения (ЛНДУ)
Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
![]() (18)
(18)
Здесь ![]() — известная функция, непрерывная на некотором промежутке.
— известная функция, непрерывная на некотором промежутке.
Согласно теореме о структуре общего решения линейного неоднородного ДУ общее решение ДУ (18) ![]() есть сумма общего решения
есть сумма общего решения ![]() соответствующего однородного уравнения (15) и любого частного решения
соответствующего однородного уравнения (15) и любого частного решения ![]() Неоднородного уравнения (18), т. е.
Неоднородного уравнения (18), т. е.
![]() (19)
(19)
Рассмотрим, в каком виде можно искать частное решение ![]() ДУ (18), когда правая часть уравнения
ДУ (18), когда правая часть уравнения ![]() имеет специальный вид.
имеет специальный вид.
Пусть ![]() и
и ![]() корни характеристического уравнения (13), а правая часть уравнения имеет вид:
корни характеристического уравнения (13), а правая часть уравнения имеет вид:
![]() (20)
(20)
Где ![]() — многочлены от Х степеней N и M соответственно с известными коэффициентами.
— многочлены от Х степеней N и M соответственно с известными коэффициентами.
Тогда частное решение ![]() следует искать в виде:
следует искать в виде:
![]() (21)
(21)
Где K — кратность корня ![]() характеристического уравнения:
характеристического уравнения:
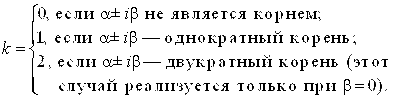
При этом ![]() Многочлены от Х степени
Многочлены от Х степени ![]() с
с
некоторыми, пока неизвестными, коэффициентами. Неизвестные коэффициенты многочленов ![]() и
и ![]() находят методом неопределенных коэффициентов.
находят методом неопределенных коэффициентов.
Пример 2.3. Найти общее решение линейных неоднородных ДУ 2-го порядка с постоянными коэффициентами:
А) ![]() б)
б) ![]()
Решение.
А) ![]()
Найдем общее решение соответствующего однородного ДУ:
![]()
Характеристическое уравнение:
![]()
Поскольку ![]() и
и ![]() то общее решение запишем в виде (17), при этом учтем, что
то общее решение запишем в виде (17), при этом учтем, что ![]()
![]()
Найдем частное решение неоднородного уравнения. Правая часть уравнения ![]()
Сравнивая ее с видом (20) ![]() заключаем, что
заключаем, что ![]() Определим параметры частного решения (21). Учитывая, что
Определим параметры частного решения (21). Учитывая, что ![]() а
а ![]() получим, что
получим, что ![]() Не является корнем характеристического уравнения, поскольку корни
Не является корнем характеристического уравнения, поскольку корни ![]() Следовательно, K = 0. Найдем
Следовательно, K = 0. Найдем ![]() Следовательно, порядок многочленов R и S Равен 0, т. е. R0 = A, а S0 = B, где А и В — некоторые неизвестные пока коэффициенты. Подставив полученные параметры в
Следовательно, порядок многочленов R и S Равен 0, т. е. R0 = A, а S0 = B, где А и В — некоторые неизвестные пока коэффициенты. Подставив полученные параметры в ![]() имеем:
имеем:
![]()
Коэффициенты А и В определим из условия, что функция УЧн — решение уравнения и поэтому должна ему удовлетворять. Найдем ![]() и
и ![]()
![]()
И подставим в исходное уравнение:
![]()
Приравняем коэффициенты при ![]() и
и ![]() в правой и левой частях полученного равенства:
в правой и левой частях полученного равенства:
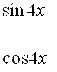

Итак, ![]()
Тогда согласно (19) общее решение неоднородного ДУ имеет вид:
![]()
Б) ![]()
Найдем общее решение соответствующего однородного ДУ:
![]()
Характеристическое уравнение:
![]()
Найдем его корни по формуле (17):

Поскольку ![]() и
и ![]() то общее решение запишем в виде (17):
то общее решение запишем в виде (17):
![]()
Найдем частное решение неоднородного уравнения. Правая часть уравнения ![]() Сравнивая ее с видом (20)
Сравнивая ее с видом (20) ![]() заключаем
заключаем ![]() Определим параметры частного решения (21). Учитывая, что
Определим параметры частного решения (21). Учитывая, что ![]() а
а ![]() получим, что
получим, что ![]() Однократный корень характеристического уравнения, поскольку корни
Однократный корень характеристического уравнения, поскольку корни ![]() Следовательно, K = 1. Найдем
Следовательно, K = 1. Найдем ![]() Следовательно, порядок многочленов R и S равен 1, т. е.
Следовательно, порядок многочленов R и S равен 1, т. е. ![]() а
а ![]() где А, В, С, D — неизвестные коэффициенты. Подставляя полученные параметры в
где А, В, С, D — неизвестные коэффициенты. Подставляя полученные параметры в ![]() имеем:
имеем:
![]()
Для определения коэффициентов А и В найдем ![]() и
и ![]()

И подставим в исходное уравнение:

Разделим обе части уравнения на ![]() и приведем подобные члены:
и приведем подобные члены:
![]()
Приравняем коэффициенты при одинаковых степенях Х в правой и левой частях уравнения:
![]()
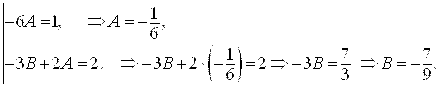
Итак, ![]()
Тогда согласно (19) общее решение неоднородного ДУ имеет вид:
![]()
| < Предыдущая | Следующая > |
|---|