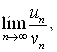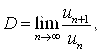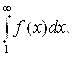17. Таблица 1. Достаточные признаки сходимости положительных рядов

Название признака

Формулировка признака

Примечание

1. Первый признак сравнения

Пусть сравниваются два положительных ряда и . Если для всех N, начиная с некоторого N, выполняются неравенства , то из сходимости «большего» ряда следует сходимость «меньшего» ряда ; если расходится «меньший» ряд ,, то расходится также «больший» ряд .

При сравнении могут полезными оказаться известные неравенства: sin a < a < tg a, если 0 < a < p/2;

Ln n < n, Если N ³ 2

2.Второй признак сравнения

Если существует конечный отличный от нуля предел

То ряды

и одновременно сходятся, либо расходятся.

В качестве эталонного ряда часто используют Обобщенный гармонический ряд S(1/np) который сходится при P>1, а расходится при P<1, а также “геометрический” ряд SQn , который сходится при ½Q½<1.

3. Признак Даламбера

Если для положительного ряда Существует конечный предел

тогда при D<1 ряд сходится, а при D>1 - расходится.

В случае D = 1 признак «не работает»; нужен другой, более сильный признак.

4. Радикальный признак Коши

Если для положительного ряда существует конечный предел

То при K<1 ряд сходится, а при K>1 – расходится.

Если K = 1, нужен другой признак

5. Интегральный признак Коши

Пусть при Х ³1 F(X) - непрерывная монотонно убывающая положительная функция, а члены ряда

Являются значениями этой функции натурального аргумента: . Тогда ряд сходится, если сходится несобственный интеграл

Если интеграл расходится, то и ряд расходится.

Интегральный признак удобно применять к исследованию положительных рядов, для которых признаки Даламбера или радикальный не приводят к цели, а несобственный интеграл легко исследовать на сходимость