17. Математическое ожидание случайной величины дискретного типа

Математическое ожидание - важнейшая “характеристика положения” случайной величины. Для дискретной величины она вычисляется по формуле

М(Х) = x1 · p1 + x2 · p2 + ... + xk · pk (+...) = ,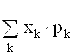

Где x1, x2, ... , xk, ... - возможные значения случайной величины (верхняя строка таблицы), p1, p2, ..., pk, ... - их вероятности (нижняя строка).

Математическое ожидание - это число, которое выражает среднее значение случайной величины (иначе, среднее значение по распределению). Для примера из §13

М(Х1) = 0 · 0,25 + 1 · 0,5 + 2 · 0,25 = 1 .

Здесь Х1 - число “орлов”, выпавших при 2 бросках симметричной монеты. М(Х1) - среднее число “орлов”, выпадающих при 2 бросках симметричной монеты, это число равно 1.

Для другого примера из §13 М(Х2) = 6.

Отметим два простейших свойства математического ожидания:

1. М (С) = С

2. М (С · Х) = С · М(Х) ( С - постоянная ).

В дальнейшем нам придется вычислять математическое ожидание случайной величины Х2. Если случайная величина Х задается таблицей

X	X1	X2	...	Xk
P	P1	P2	...	Pk

То случайная величина Х2 получится после возведения в квадрат возможных значений случайной величины Х, при этом Р(Х = хк)= = Р(Х2 = хк2) = pk :

X2	X12	X22	...	Xk2
P	P1	P2	...	Pk

Поэтому М(Х2) = x12 · p1 + x22 · p2 + ... + xk2 · pk = .

В частности, для примера из §13

X2	02	12	22
P	0,25	0,5	0,25

И М(Х2) = 02 · 0,25 + 12 · 0,5 + 22 · 0,25 = 1,5

< Предыдущая		Следующая >