16. Функция распределения

Если F(x) = P(X < x), то функция F(x) называется функцией распределения (интегральной функцией распределения) случайной величины Х, т. е. функция распределения в точке “х” - это вероятность того, что случайная величина Х примет значение, меньшее заданного числа х.

Из определения сразу следуют несколько свойств F(x):

F(- ¥) = 0, F(+ ¥ ) = 1;

F(x) - неубывающая функция (т. е. если x1 < x2 , то F(x1) £ F(x2) ).

Функция распределения для случайной величины дискретного типа имеет “ступенчатый” график. Для случайной величины Х1 из §13 F(x) запишется так:

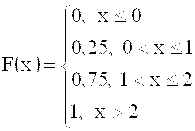
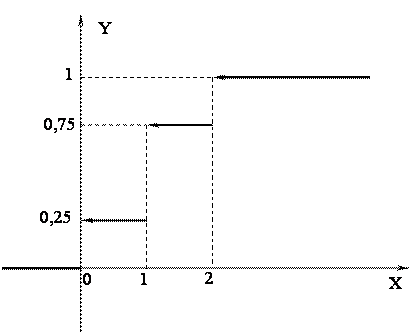
Обратите внимание, что левые концы «ступенек» - выколотые, а правые - нет. Например, F(1) = P(X1 < 1) = P(X1 =0) = 0,25;

F(1,1) = P(X1<1,1) = P(X1 = 0) + P(X1 = 1) = 0,75. «Высоты» «ступенек» равны очередным вероятностям, взятым из таблицы : сначала 0,25, затем еще +0,5, и наконец еще +0,25.

Аналогичный график и для другого примера – про домино – только там будет не 2, а 12 «ступенек».

Справедлива формула: P(a £ X < b) = F(b) - F(a).

< Предыдущая		Следующая >