12. Элементарные преобразования матрицы

Если размеры матрицы большие, то ранг матрицы вычисляют, пользуясь методом элементарных преобразований. Этот метод является универсальным и используется также для исследования и решения систем уравнений, вычисления определителей и обращения матриц.

Элементарными преобразованиями матрицы называют следующие:

Перестановка строк (столбцов) матрицы;

Умножение строки (столбца) на число отличное от нуля;

Прибавление к элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

Целью элементарных преобразований является приведение исходной матрицы к ступенчатой форме. Матрица называется ступенчатой, если для нее выполняются следующие условия:

Если какая – либо строка матрицы состоит из нулей, то и все последующие строки также состоят из нулей;

Если первый, отличный от нуля, элемент какой – либо строки расположен в одном из столбцов данной матрицы, то все элементы этого столбца, расположенные ниже, являются нулевыми.

Матрица из одной строки считается ступенчатой по определению.

Например, матрица 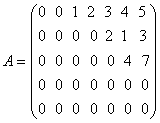является ступенчатой.

Теорема (о приведении к ступенчатой матрице).

Любую матрицу можно привести к ступенчатой матрице, выполнив конечное число элементарных преобразований.

Теорема доказывается конструктивно путем перебора конечного числа возможных матриц с нулевыми элементами.

Пример. Приведем к ступенчатому виду следующую матрицу: .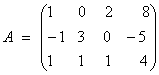

На первом шаге выполним следующие элементарные преобразования над матрицей : к элементам второй строки прибавим элементы первой строки и результат запишем во вторую строку; из элементов третьей строки вычтем элементы первой строки, а результат запишем в третью строку. В итоге матрица преобразуется к виду 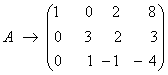. На последнем шаге из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, и запишем в третью строку, в результате чего получим ступенчатую матрицу:

.

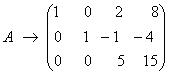Теорема (о ранге ступенчатой матрицы).

Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Доказательство. Ненулевые, ступенчатые строки линейно независимы, что можно показать, составив линейную комбинацию этих строк и приравняв ее нулевой строке. Покомпонентный анализ этой линейной комбинации показывает, что все числовые коэффициенты при строках, начиная с первой, последовательно обращаются в нули. По определению это означает линейную независимость ненулевых строк. Остальные строки ступенчатой матрицы нулевые, а добавление нулевой строки в систему ненулевых строк превращает новую систему в зависимую систему. Поэтому только ненулевые строки линейно независимы. По следствию 1 теоремы о базисном миноре это означает, что ранг ступенчатой матрицы равен числу ее ненулевых строк, что и требовалось доказать.

Теорема (об элементарных преобразованиях).

Ранг матрицы не изменяется при ее элементарных преобразованиях.

Доказательство. При любых элементарных преобразованиях отличный от нуля определитель остается таковым. Поэтому любой найденный базисный минор останется базисным. Миноры более высокого порядка равны нулю и останутся таковыми при любых элементарных преобразованиях. Таким образом, теорема доказана.

На основе трех, приведенных выше теорем, формулируется метод элементарных преобразований: сначала исходная матрица приводится к ступенчатому виду, затем ранг исходной матрицы полагается равным числу ненулевых строк ступенчатой матрицы.

В рассмотренном выше примере матрица была приведена элементарными преобразованиями к ступенчатой матрице, имеющей три ненулевые строки. Это означает, что ранг исходной матрицы равен трем.

Исследуя систему уравнений общего вида, необходимо либо доказать, что она не имеет решений, либо, если она совместна, найти все возможные решения и представить их в компактной и наглядной форме. Для этого систему уравнений с помощью элементарных преобразований приводят к более простому виду, позволяющему непосредственно увидеть решения или показать несовместность системы. При этом центральным понятием является равносильность двух систем. Две системы уравнений с одними теми же неизвестными называются равносильными, если они имеют одно и то же множество решений.

Например, системы 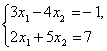и 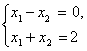являются равносильными, так как каждая из них имеет одно и то же единственное решение .

Системы 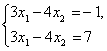и также являются равносильными, поскольку каждая из них не имеет решений (множество решений пусто).

Элементарными преобразованиями системы линейных алгебраических уравнений называют следующие преобразования:

Перестановка местами любых двух уравнений;

Умножение любого уравнения системы на одно и то же число, отличное от нуля;

Сложение любых двух уравнений.

Теорема (о равносильных переходах).

Любое конечное число элементарных преобразований системы переводят ее в систему, равносильную исходной системе.

Доказательство теоремы следует непосредственно из определения элементарных преобразований системы линейных уравнений общего вида.

Как видно из приведенных определений, элементарным преобразованиям системы полностью соответствуют элементарные преобразования строк так называемой

Расширенной матрицы системы , которая получается из матрицы коэффициентов системы добавлением - го столбца, состоящего из правых частей уравнений системы.

< Предыдущая		Следующая >