13. Метод Гаусса
На приведении расширенной матрицы системы к ступенчатым матрицам специального вида основан метод решения систем линейных уравнений, называемый методом Гаусса или методом последовательного исключения неизвестных.
На первом этапе (прямой ход метода Гаусса) расширенная матрица ![]() Приводится к ступенчатой матрице
Приводится к ступенчатой матрице ![]() , у которой все ненулевые строки имеют первый элемент, равный единице. Решение полученной системы уравнений с расширенной ступенчатой матрицей
, у которой все ненулевые строки имеют первый элемент, равный единице. Решение полученной системы уравнений с расширенной ступенчатой матрицей ![]() называется обратным ходом метода Гаусса. Обратный ход может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего, так и в форме последующего преобразования матрицы
называется обратным ходом метода Гаусса. Обратный ход может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего, так и в форме последующего преобразования матрицы ![]() к ступенчатой матрице
к ступенчатой матрице ![]() , у которой все ненулевые строки содержат только одну единицу и позволяют в явном виде представить решение системы.
, у которой все ненулевые строки содержат только одну единицу и позволяют в явном виде представить решение системы.
Отметим, что, выполняя прямой ход метода Гаусса, мы получаем возможность эффективного вычисления ранга матрицы и определителя. Если нас интересует ранг матрицы, то после преобразования ее к ступенчатой форме, достаточно подсчитать число ненулевых строк: это и будет ранг матрицы.
Если нас интересует определитель матрицы, то эта матрица, естественно, должна быть квадратной. После преобразования ее методом Гаусса к ступенчатой форме она примет вид верхней треугольной матрицы, то есть матрицы, у которой все элементы ниже главной диагонали равны нулю. Определитель любой верхней треугольной матрицы равен произведению всех элементов, стоящих на главной диагонали. Если на главной диагонали имеется хотя бы один нулевой элемент, то определитель треугольной матрицы равен нулю и, соответственно, определитель исходной матрицы равен нулю. Если же на главной диагонали в результате преобразований прямого хода метода Гаусса окажутся только единицы, то надо в процессе преобразований следить за перестановками строк, которые изменяют знак определителя на обратный, и за умножениями или делениями строк матрицы на числа, которые пропорционально изменяют величину определителя. Определитель исходной матрицы находится как произведение всех чисел, на которые делились строки. Знак этого произведения остается прежним, если было проведено четное число перестановок строк, и изменяется на противоположный, если число перестановок строк было нечетным.
Пример. Решим методом Гаусса следующую систему: 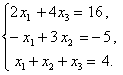
Выполняя прямой ход метода Гаусса, приведем расширенную матрицу этой системы  к ступенчатой матрице, у которой все ненулевые строки имеют первый ненулевой элемент, равный единице. На первом этапе выполним следующие элементарные преобразования исходной расширенной матрицы: разделим первую строку на число два; сложим вторую строку с первой и результат запишем во вторую строку; из третьей строки вычтем преобразованную первую строку и результат запишем в третью строку:
к ступенчатой матрице, у которой все ненулевые строки имеют первый ненулевой элемент, равный единице. На первом этапе выполним следующие элементарные преобразования исходной расширенной матрицы: разделим первую строку на число два; сложим вторую строку с первой и результат запишем во вторую строку; из третьей строки вычтем преобразованную первую строку и результат запишем в третью строку:

![]()
 .
.
Мы получили в результате, что первая строка ненулевая, имеет первым ненулевым элементом число один, а все элементы в первой колонке под числом один равны нулю. Для того чтобы, вторая строка начиналась с единицы, переставим вторую и третью строки местами:

![]()
 .
.
Для того чтобы под единицей во втором столбце стоял нуль, из третьей строки полученной матрицы вычтем вторую строку, умноженную на три, и запишем в третью строку:

![]()
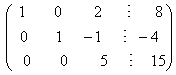 .
.
Наконец, чтобы третья строка имела первым ненулевым элементом число один, поделим третью строку на число пять:
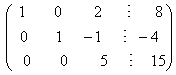
![]()
 =
=![]() .
.
На этом завершается прямой ход метода Гаусса, а преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице, равносильна исходной системе уравнений и имеет следующий вид:
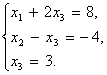
Отметим, что, выполняя прямой ход метода Гаусса, мы получаем возможность эффективного вычисления ранга матрицы и определителя. Если нас интересует ранг матрицы, то после преобразования ее к ступенчатой форме, достаточно подсчитать число ненулевых строк: это и будет ранг матрицы.
Если нас интересует определитель матрицы, то эта матрица, естественно, должна быть квадратной. После преобразования ее методом Гаусса к ступенчатой форме она примет вид верхней треугольной матрицы, то есть матрицы, у которой все элементы ниже главной диагонали равны нулю. Определитель любой верхней треугольной матрицы равен произведению всех элементов, стоящих на главной диагонали. Если на главной диагонали имеется хотя бы один нулевой элемент, то определитель треугольной матрицы равен нулю и, соответственно, определитель исходной матрицы равен нулю. Если же на главной диагонали в результате преобразований прямого хода метода Гаусса окажутся только единицы, то надо в процессе преобразований следить за перестановками строк, которые изменяют знак определителя на обратный, и за умножениями или делениями строк матрицы на числа, которые пропорционально изменяют величину определителя. Определитель исходной матрицы находится как произведение всех чисел, на которые делились строки. Знак этого произведения остается прежним, если было проведено четное число перестановок строк, и изменяется на противоположный, если число перестановок строк было нечетным.
В нашем примере, выполнив прямой ход метода Гаусса, мы одновременно нашли ранг матрицы коэффициентов системы (![]() , так как число ненулевых строк преобразованной матрицы
, так как число ненулевых строк преобразованной матрицы ![]() равно трем), а также ранг расширенной матрицы (
равно трем), а также ранг расширенной матрицы (![]() , так как число ненулевых строк преобразованной матрицы
, так как число ненулевых строк преобразованной матрицы ![]() равно трем).
равно трем).
Для вычисления определителя исходной матрицы коэффициентов необходимо обратить внимание на три обстоятельства: вид верхней треугольной матрицы, в которую преобразовалась исходная матрица; на какие числа делились или умножались строки; какое количество (четное или нечетное) перестановок было выполнено в процессе преобразований. Так как на главной диагонали стоят только единицы, то определитель не равен нулю. Далее в процессе преобразований было использовано деление на число 2 первой строки и деление на число 5 третьей строки. Их надо перемножить ![]() и подсчитать число перестановок строк местами: была выполнена одна перестановка. Таким образом, определитель матрицы коэффициентов равен:
и подсчитать число перестановок строк местами: была выполнена одна перестановка. Таким образом, определитель матрицы коэффициентов равен: ![]() .
.
Выполним обратный ход метода Гаусса сначала первым способом, то есть последовательно определим неизвестные, начиная с последнего уравнения:
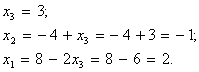
Выполним обратный ход метода Гаусса вторым способом. Продолжим элементарные преобразования матрицы ![]() и приведем ее к ступенчатой матрице
и приведем ее к ступенчатой матрице ![]() , у которой все ненулевые строки содержат только одну единицу. Это позволит в явном виде представить решение системы. Сложим вторую строку с третьей строкой и результат запишем во вторую строку:
, у которой все ненулевые строки содержат только одну единицу. Это позволит в явном виде представить решение системы. Сложим вторую строку с третьей строкой и результат запишем во вторую строку:
![]() =
=
![]()
 .
.
Далее, чтобы заменить число два первой строки на число нуль, умножим третью строку на число (-2), сложим с первой строкой и результат запишем в первую строку:

![]()
 .
.
На этом заканчивается обратный ход метода Гаусса. Преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице типа![]() , равносильна исходной системе уравнений и имеет следующий вид
, равносильна исходной системе уравнений и имеет следующий вид

Который представляет собой запись решения системы в явной форме.
Для исследования решения систем линейных уравнений с произвольным числом уравнений и неизвестных полезна следующая теорема.
| < Предыдущая | Следующая > |
|---|