11. Базис множества векторов и всего линейного пространства

Система векторов называется базисом множества , если:

Все векторы системы принадлежат множеству ;

Система векторов является линейно независимой системой;

Любой вектор из множества представим в виде линейной комбинации векторов этой системы, т. е. .

Если множество Совпадает со всем пространством , то базис является базисом всего линейного пространства.

Числа Называются координатами вектора В базисе , а выражение - разложением вектора По базису .

Теорема (о единственности разложения по данному базису).

Разложение любого вектора по базису является единственным.

Доказательство. Предположим, что для вектора Наряду с разложением имеется другое разложение . Вычитая одно разложение из другого, получим равенство .

Поскольку базисные векторы линейно независимы, то из полученного равенства следуют равенства , что и доказывает теорему.

Следствие. Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.

Таким образом, при фиксированном базисе линейного пространства каждый вектор однозначно определяется своими координатами в этом базисе.

Теорема (о линейных свойствах координат векторов).

При сложении любых двух векторов их координаты в данном базисе складываются, а при умножении любого вектора на любое число координаты умножаются на это число.

Доказательство. Пусть любые два вектора Имеют в базисе разложения , . Из аксиом линейного пространства следует, что сумма векторов И произведение вектора на число представимы в виде , .

Отсюда и теоремы о единственности разложения векторов по данному базису следует истинность доказываемой теоремы.

Теорема о базисном миноре.

Базисные строки (столбцы) линейно независимы и образуют базис в системе всех строк (столбцов) произвольной матрицы размера .

Доказательство.

По определению базиса это означает, что любая строка или столбец матрицы могут быть представлены в виде линейной комбинации базисных строк или базисных столбцов, причем единственным образом. Все рассуждения достаточно провести для строк, так как, транспонировав исходную матрицу, мы получим доказательство для столбцов матрицы .

Линейную независимость базисных строк будем доказывать методом от обратного.

Пусть некоторые базисные строки линейно зависимы. Тогда одна из этих строк является линейной комбинацией остальных строк. Но тогда из свойств определителей следует, что базисный минор равен нулю. Базисный минор по определению не должен быть равен нулю. Таким образом, исходное предположение ложно и базисные строки линейно независимы.

Докажем теперь, что любая строка произвольной матрицы размера является линейной комбинацией базисных строк. Для удобства в обозначениях будем считать, что базисный минор стоит на пересечении первых строк и первых столбцов. Это предположение не ограничивает общности доказательства теоремы, так как всегда можно переставить базисные строки и столбцы таким образом, чтобы базисный минор находился в левом верхнем углу матрицы . При таких перестановках может измениться знак определителя, но он не может стать равным нулю, что изменило бы ранг матрицы.

Пусть – любое число от 1 до , а – любое число от 1 до . Убедимся в том, что любой определитель порядка :

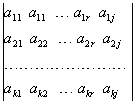
Равен нулю. Если или , то указанный определитель будет равен нулю в силу того, что у него будет два одинаковых столбца или две одинаковые строки. Если оба числа и Строго больше , то любой указанный определитель будет иметь порядок , и равен нулю по определению базисного минора. Таким образом, при любых значениях и наш определитель всегда нулю. Разложим этот определитель по последнему столбцу:

.

Алгебраические дополнения к элементам последнего столбца с номером ,очевидно, не зависят от элементов с номерами, содержащими . Поэтому в крайней правой части нашего разложения они обозначены буквами , не включающими индекс . Значение всегда не равно нулю, так как оно с точностью до знака совпадает со значением базисного минора. Разделив последнее равенство на число , мы получим, что

.

Эти равенства справедливы для любых чисел и , и означают, что любая строка с номером Является линейной комбинацией первых базисных строк. Таким образом, теорема полностью доказана.

Из теоремы о базисном миноре вытекают два важных следствия.

1. Для любой матрицы число линейно независимых строк равно числу линейно независимых столбцов и равно рангу матрицы.

2. Определитель любого порядка равен нулю тогда и только тогда, когда его строки или его столбцы линейно зависимы.

Отметим, что по закону контрпозиции равносильное свойству 2 утверждение формулируется следующим образом: определитель отличен от нуля тогда и только тогда, когда его строки или его столбцы линейно независимы.

Доказательство.

Покажем достаточность условия второго следствия. Если строки матрицы линейно зависимы, то по свойству системы зависимых векторов одна из строк является линейной комбинацией остальных строк. Вычитая из этой строки указанную линейную комбинацию, мы, не изменяя величины определителя, получим матрицу, содержащую нулевую строку. Определитель такой матрицы всегда равен нулю, что и требовалось доказать.

Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимым для равенства нулю определителя матрицы. Если определитель порядка равен нулю, то его базисный минор имеет порядок, заведомо меньший . Но тогда хотя бы одна из строк является не базисной. По теореме о базисном миноре эта строка может быть представлена в виде линейной комбинации базисных строк, что и означает линейную зависимость всех строк исходной матрицы. Следствие полностью доказано.

< Предыдущая		Следующая >