09. Ранг матрицы, пример

Для исследования и решения систем линейных уравнений в общем виде введем предварительно понятие о ранге матрицы.

Пусть в матрице размера произвольно выбраны строк и столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка , определитель которой называется минором порядка матрицы .

Базисным минором произвольной матрицы размера Называют любой ее минор порядка , если он отличен от нуля, а все миноры порядка либо равны нулю, либо не существуют (выходят за размеры исходной матрицы ). Порядок базисного минора называется рангом матрицы и обозначается .

Строки и столбцы, на пересечении которых находится базисный минор, называются базисными строками и базисными столбцами.

Отметим, что у матрицы может быть несколько базисных миноров, причем каждому из них соответствуют свои базисные строки и столбцы. Если матрица является квадратной порядка и невырожденной, то по определению ее ранг равен числу , то есть , так как определитель порядка отличен от нуля, а других определителей более высокого порядка не существует. Все строки и все столбцы такой матрицы являются базисными.

Если размеры матрицы не очень большие, то ранг матрицы вычисляют, пользуясь методом окаймляющих миноров.

Пусть в матрице найден некоторый минор порядка , отличный от нуля. Рассмотрим лишь те миноры порядка , которые содержат в себе (окаймляют) выделенный минор. Если все окаймляющие миноры равны нулю, то ранг матрицы равен . Если же среди окаймляющих миноров найдется ненулевой минор порядка , то процедура повторяется, пока ранг не будет найден.

Пример. Найдем методом окаймляющих миноров ранг следующей матрицы

.

Фиксируем минор порядка два, отличный от нуля, , стоящий в первых двух строках, и в третьем и четвертом столбцах матрицы.

Минор порядка три, стоящий в левом верхнем углу, окаймляет предшествующий минор и также отличен от нуля. Однако, оба возможных окаймляющих минора порядка четыре равны нулю:

.

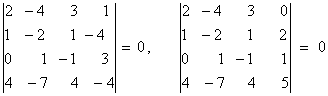Таким образом, ранг матрицы найден по методу окаймляющих миноров и равен трем.

< Предыдущая		Следующая >