08. Теорема Крамера

Если в квадратной системе уравнений определитель матрицы коэффициентов не равен нулю, то система имеет единственное решение, которое находится либо матричным способом по формуле , либо по формулам Крамера ,

Где матрицы получены из матрицы заменой -тых столбцов на столбец правых частей системы.

Доказательство.

В соответствии с теоремой о существовании и единственности обратной матрицы, для невырожденной матрицы коэффициентов нашей системы существует единственная обратная матрица . Умножая нашу систему, имеющую в матричной форме вид , слева на обратную матрицу , получим: .

Таким образом, доказано, что матричным способом вектор – столбец решений Находится в единственном виде по формуле .

Если далее формулу представить в покомпонентной записи, то для компонент вектора неизвестных будем иметь формулы

,,

Так как суммы в круглых скобках представляют собой разложения определителей по -тым столбцам матриц .

Таким образом, теорема Крамера полностью доказана.

Решим для примера следующую систему уравнений:

Матрица коэффициентов этой системы 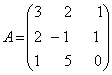неособенная, так как . Присоединенная матрица Имеет вид . Отсюда , ,

Т. е. .

Если ту же систему уравнений решать с помощью формул Крамера, то:

,

,

.

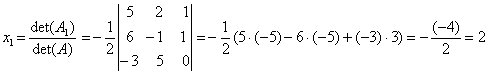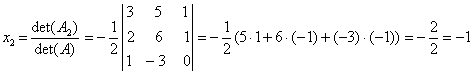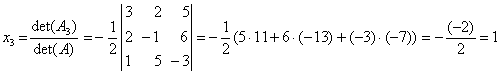Отметим, что в нашем примере мы находили определители в числителях формул Крамера, используя разложения по столбцам свободных членов. Однако, как следует из теоремы о разложении определителя по любым строкам или столбцам, можно было выбрать любые удобные строки или столбцы.

< Предыдущая		Следующая >