06. Системы линейных уравнений

Общая система из линейных алгебраических уравнений с неизвестными Имеет вид

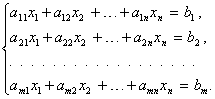
Коэффициенты при неизвестных объединяют в так называемую матрицу системы 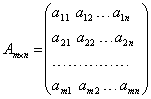, неизвестные – в матрицу – столбец неизвестных 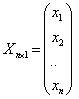, а правые части уравнений объединяют в матрицу – столбец 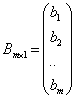. Учитывая введенные обозначения и определения умножения и равенства матриц, исходную систему уравнений записывают в виде .

Обычно, для более краткой записи нижние индексы матриц опускают и систему уравнений в матричной форме представляют в виде .

Если все правые части уравнений равны нулю, то систему называют однородной, если же хотя бы одна из правых частей системы отлична от нуля, то систему называют неоднородной. Если число уравнений равно числу неизвестных, то матрица ее коэффициентов квадратная, а саму систему называют квадратной.

Конечная последовательность чисел Называется решением системы уравнений, если при подстановке этих чисел вместо неизвестных Все уравнения системы обращаются в верные равенства. Множество всех решений системы называют общим решением системы.

Система уравнений называется совместной, если она имеет хотя бы одно решение. В обратном случае систему называют несовместной, а ее множество решений является пустым множеством. Если решение системы единственное, то такую систему называют определенной, если же система имеет более чем одно решение, то – неопределенной. Далее будет доказано, что неопределенные системы могут иметь только бесконечно много решений. Таким образом, любая система может иметь одно решение, бесконечно много решений или не иметь вообще ни одного решения.

Рассмотрим несколько характерных примеров.

Система уравнений 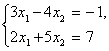- квадратная, неоднородная, имеет единственное решение , так что является определенной. Система 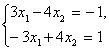имеет более одного решения. Например, ее решениями являются значения: ; ; . Такая система называется неопределенной. Система 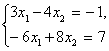не имеет ни одного решения. Такая система называется несовместной.

Исследование линейных систем начнем с решения квадратных систем. Введем предварительно необходимые определения. Если определитель матрицы не равен нулю, то такие матрицы будем именовать неособенными или невырожденными. Если же определитель матрицы равен нулю, то такую матрицу будем называть особенной или вырожденной.

< Предыдущая		Следующая >