04. Матрицы и операции над ними

Матрицы и определители матриц широко используются при решении систем линейных уравнений, линейном программировании, исследовании систем дифференциальных уравнений. Аппарат теории матриц применяется в вычислительной математике, физике, моделировании практических задач в технике, экономике и бизнесе.

Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Матрицы обычно обозначают заглавными буквами латинского алфавита в виде , если важно знать ее размеры, или буквами . Записывается матрица в следующем виде .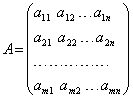

Элементы матрицы нумеруются двумя индексами. Первый индекс обозначает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент в матрице. Матрица называется числовой, если ее элементы вещественные или комплексные числа; функциональной, если ее элементы – функции; блочной, если ее элементы – другие матрицы. Если число строк матрицы равно числу ее столбцов, то матрицу называют квадратной. Все элементы квадратной матрицы, которые имеют одинаковые первые и вторые индексы, образуют главную диагональ матрицы. Если матрица имеет только одну строку, то ее называют матрицей – строкой или вектор – строкой. Такая матрица совпадает с арифметическим вектором, и ее элементы отделяют друг от друга запятыми. Если матрица имеет только один столбец, то ее называют матрицей – столбцом или вектор – столбцом. По соглашению, арифметические векторы записывают в виде вектор – столбцов. Например, матрица - прямоугольная числовая матрица размером две строки на три столбца, матрица - квадратная числовая матрица размером две строки на два столбца, матрица - это матрица – строка, а матрица - матрица – столбец.

Некоторые матрицы имеют специальные обозначения и названия.

Произвольная матрица называется нулевой, если все ее элементы равны нулю. Например, матрица – нулевая размером два на три.

Квадратная матрица называется единичной, если все ее элементы на главной диагонали равны единице, а все остальные элементы равны нулю. Так, матрица - единичная и имеет размеры два на два.

Квадратная матрица называется диагональной, если ее элементы, стоящие выше и ниже главной диагонали равны нулю. Например, матрица 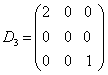- диагональная.

Если в матрице размером заменить строки на столбцы с тем же номером, то получится новая матрица размером , которую называют транспонированной к исходной матрице . Таким образом, по определению для всех элементов транспонированной матрицы выполняются соотношения: . Например, транспонированной по отношению к матрице размером две строки на три столбца будет матрица размером три строки на два столбца. Если дважды транспонировать матрицу, то в результате получится исходная матрица.

Матрицы и Называют равными, если они имеют одинаковые размеры и все их соответствующие элементы равны, т. е. , если .

Например, числовая матрица равна квадратной, функциональной матрице 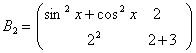, но они записаны в различных формах.

Квадратная матрица Называется симметричной, если она совпадает с транспонированной матрицей, т. е. . Например, матрица - симметричная, и видно, что она симметрична относительно главной диагонали. Отметим также, что диагональная и единичная матрицы являются симметричными, так как они совпадают со своими транспонированными матрицами, что проверяется непосредственно.

Для матриц введены две основные операции: сложение матриц и умножение матрицы на число (вещественное или комплексное).

Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть .

Так, если и , то .

Для операции сложения матриц выполняются свойства коммутативности И ассоциативности , которые следуют из соответствующих свойств чисел. Если к любой матрице прибавить слева или справа нулевую матрицу, то исходная матрица не изменится; таким образом, выполняются равенства . Для любой матрицы существует единственная противоположная матрица , такая что , что также следует из аксиоматических свойств чисел. Разность двух матриц одинаковых размеров определяется как обычно по правилу , то есть соответствующие элементы первой и второй матриц вычитаются. Так, если

и , то .

Произведением матрицы на число (вещественное или комплексное) называется матрица , полученная из исходной матрицы умножением всех ее элементов на число , то есть .

Например, пусть . Тогда .

Для основных матричных операций выполняются, дополнительно к вышеуказанным четырем свойствам, следующие четыре свойства:

- при умножении на число 1 матрица не изменяется ,

- ассоциативность умножения на числа ,

- две дистрибутивности и . Все свойства матриц следуют из соответствующих свойств чисел.

Таким образом, для матриц относительно основных операций сложения и умножения на число выполняются все восемь аксиом линейного пространства. Это позволяет считать матрицы элементами некоторого конкретного линейного пространства и обращаться с ними как с векторами. Отметим, что арифметические векторы по их определению совпадают с матрицами – строками или матрицами – столбцами. Следовательно, арифметические векторы также удовлетворяют всем восьми свойствам абстрактного линейного пространства и могут, как и матрицы, называться векторами.

Операция умножения первой матрицы на вторую матрицу Не является основной. Эта операция определяется только в том случае, когда число столбцов первой равно числу строк второй (длина строк первой матрицы равна высоте столбцов второй матрицы).

Произведением матрицы размера на матрицу размера называется матрица размера , все элементы которой находятся по формулам

.

Таким образом, для нахождения элементов последовательно выбираются строки и столбцы, причем при каждом выборе элементы строки умножаются на соответствующие элементы столбца и все такие парные произведения складываются. Пусть, например, первая матрица имеет размер две строки на два столбца, вторая матрица- такой же размер. Тогда матрица , равная их произведению , находится по определяющим формулам в виде и также имеет размер две строки на два столбца. Так как матрицы И Квадратные, то их можно перемножить в обратном порядке, то есть найти

.

Мы получили в нашем случае, что . Этот контрпример доказывает, что в общем случае умножение матриц не подчиняется закону коммутативности. Существуют матрицы, для которых свойство коммутативности выполняется. Такие матрицы называют коммутирующими, и они обязательно должны быть квадратными.

Покажем, например, что матрицы и коммутирующие. Действительно

,

,

Что и доказывает наше утверждение.

Если матрица Не является квадратной, то есть , то ее нельзя умножить саму на себя, так как число столбцов первой матрицы не будет равно числу строк второй матрицы. Однако если ее транспонировать, то определено как произведение размера , так и произведение размера . Рассмотрим для примера матрицу – строку вида . Транспонированная к ней матрица будет матрицей – столбцом вида 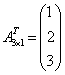. Произведение будет иметь размер три на три, а произведение будет иметь размер одна строка на один столбец. Сформируем далее матрицу

.

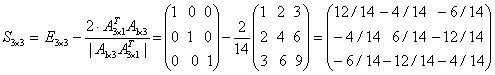В этой формуле символом обозначен определитель матрицы , состоящей из одного элемента. Как показывается ниже, определитель такой матрицы равен значению этого единственного элемента. Полученная матрица симметричная и при умножении на себя дает единичную матрицу.

Основные свойства, связанные с умножением матриц, доказываются в общем виде на основе соответствующих свойств чисел путем непосредственного сопоставления матриц слева и справа от знака равенства:

1) ,

2) ,

3) ,

4) ,

5) ,

6) .

< Предыдущая		Следующая >