8.4. Комплексные числа
Множество R действительных чисел «ведет себя идеально» по отношению ко всем арифметическим операциям в том смысле, что при сложении, вычитании, умножении и делении двух действительных чисел снова получается действительное число. Однако квадратные корни можно извлекать только из положительных действительных чисел. Этот факт создает большие неудобства, в частности, при решении алгебраических уравнений. Вы знаете, например, что квадратное уравнение имеет действительные корни тогда и только тогда, когда его дискриминант является неотрицательным. Таким образом, одни уравнения имеют два корня, а другие — ни одного. Аналогично обстоит дело и с уравнениями других степеней. Например, уравнение Х3 = 1 имеет только один действительный корень Х = 1, а уравнение Х3 – 7Х + 6 = 0 — три корня: 1, 2, –3.
Но уже в XVI в. математики поняли, каким образом можно записать решения любого квадратного уравнения, даже с отрицательным дискриминантом. История началась с того, что в 1545 г. итальянский математик Кардано опубликовал формулу для вычисления корней кубического уравнения. Однако в некоторых случаях эта формула давала странный результат. Например, корень –3 уравнения Х3 – 7Х + 6 = 0 с помощью формулы Кардано записывается таким образом:
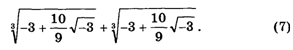
Получалось, что это выражение имеет смысл несмотря на то, что содержит квадратный корень из отрицательного числа! Объяснение нашел другой итальянский математик XVI в. Рафаэль Бомбелли. В 1572 г. он опубликовал книгу «Алгебра», в которой изложил теорию Комплексных чисел. Мы расскажем об основных идеях этой теории, используя современную математическую терминологию.
Обозначим выражение ![]() буквой I,
буквой I,
![]() ,
,
И назовем его Мнимой единицей. Мнимая единица не является действительным числом, но мы распространим на нее все алгебраические свойства действительных чисел. Будем считать, по определению, что мнимую единицу можно умножать на действительные числа и прибавлять к действительным числам. Таким образом, мы. расширили поле действительных чисел, добавив к нему новый элемент i. В результате появились другие новые элементы, которые записывают в виде А + Bi и называют Комплексными числами. Комплексное число А + Bi получается, если мнимую единицу I умножить на действительное число B и прибавить к результату действительное число А. Если B = 0, то комплексное число является действительным. Следовательно, действительные числа составляют часть комплексных чисел. Положим также, по определению, что
![]() .
.
Комплексные числа будем складывать и умножать по следующим правилам:
![]()
Заметим, что правая часть второго равенства получается как результат почленного перемножения и приведения подобных членов с учетом равенства I2 = –1. Например,
![]()
Для каждого комплексного числа можно найти ему обратное. Например,
![]()
Операции сложения и умножения комплексных чисел подчиняются аксиомам (1), откуда следует, что множество всех комплексных чисел образует Поле. Поскольку оно содержит все действительные числа, то говорят, что Поле комплексных чисел получено расширением поля действительных чисел.
С помощью комплексных чисел можно записать корни любого квадратного уравнения (это впервые сделал Бомбелли). Например, уравнение Х2 = –1 имеет корни I и –I, т. к. (±I)2 = –1; корни уравнения Х2 – х + 1 = 0 записываются следующим образом:
![]()
Теперь мы можем объяснить, почему сумма (7) будет действительным числом. Первый из двух кубических корней представляет собой комплексное число ![]() , второй
, второй ![]() (проверьте это возведением в куб!). Их сумма равна –3.
(проверьте это возведением в куб!). Их сумма равна –3.
Хотя комплексные числа были открыты в XVI в., по-настоящему их роль поняли значительно позже, в начале XIX в. Этому предшествовал ряд замечательных открытий в математике. Вот некоторые из них.
В конце XVIII в. Гаусс дал строгое доказательство так называемой основной теоремы алгебры.
Основная Теорема Алгебры: Всякое алгебраическое уравнение степени п с комплексными коэффициентами имеет ровно п комплексных корней.*
* Поэтому о поле комплексных чисел говорят, что оно является Алгебраически замкнутым.
Иоганн Бернулли и Леонард Эйлер открыли формулу
ЕIA = cos a + I sin a,
Из которой при a = p получается удивительное соотношение
ЕIA = –1,
Связывающее мнимую единицу I с тремя замечательными числами Е, p и 1.
Наконец, ряд математиков, в том числе и Гаусс, начали представлять комплексные числа геометрически, как точки плоскости. При этом комплексному числу А + Bi Соответствует точка с координатами (а, b).
Комплексные числа применяются во многих разделах математики, физики, механики и т. д. Вот несколько примеров из истории развития авиации. В начале XX в. века русский ученый Н. Е. Жуковский, которого называют отцом авиации, в своих теоретических разработках нашел некоторые виды сложных траекторий полета самолета, которые впоследствии были названы фигурами высшего пилотажа. Вскоре после этого одну из таких фигур выполнил известный летчик П. Н. Нестеров. В честь его она так и называется: петля Нестерова.
Другой русский ученый М. В. Келдыш (впоследствии Президент Академии наук СССР) решил проблему Флаттера (внезапная вибрация самолета, приводящая к его разрушению во время полета), проблему Шимми (разрушение колес при посадке самолета). Оба ученых пользовались в своих расчетах методами комплексного анализа.
| < Предыдущая | Следующая > |
|---|