8.3. Группы

Нетрудно заметить, что система аксиом кольца (1) и система аксиом векторного пространства (2) имеют неко­торую общую часть. Три свойства операции сложения:

Ассоциативность: (а + B) + с = а + (B + с),

Наличие нейтрального элемента: А + 0 = а,

Существование противоположных элементов: А + (-а) = 0 (3)

Справедливы для любого кольца и любого векторного пространства. Приведем еще примеры математических объектов, обладающих подобными свойствами.

I. Запишем по порядку числа 1, 2, 3, 4, 5, 6. Теперь перепутаем их каким-либо образом: 2, 3, 5, 1, 6, 4. Ре­зультат нашей деятельности запишем в виде таблицы:

Эта таблица задает некоторую функцию, если считать, что верхний ряд — значения независимого переменного Х, а нижний — соответствующие значения зависимого переменного У. Такая функция называется Подстанов­кой или перестановкой из шести элементов и действует вполне понятным образом: единицу переводит в двойку, двойку — в тройку, тройку — в пятерку, четверку — в единицу, пятерку — в шестерку а шестерку — в четвер­ку. Всего подстановок из шести элементов будет 6! = 1 • 2 • 3 • 4 • 5 • 6 = 720 штук (см. гл. III, §3).

Результат последовательного действия двух перестановок тоже будет перестановкой. Запись

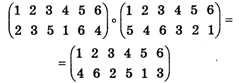
Показывает, что в результате последовательного действия перестановок

Получилась перестановка

В самом деле, первая из них переводит единицу в двой­ку, а вторая переводит двойку в четверку. Следователь­но, в результате совместных усилий они переводят еди­ницу в четверку. Остальное аналогично.

Результат последовательного действия двух функций называется их Композицией или Сложной функцией.* Но по отношению к перестановкам допускается некото­рая вольность речи. Говорят, что перестановка S явля­ется Произведением перестановок S1 и S2.

* Сравните с определением сложной функции, приведенном в гл. V, §5.

Три любые перестановки S1, S2 и S3 можно перемножить либо так: , либо так: . Но результат получится один и тот же, поскольку в обоих случаях перестановки S1, S2 и S3 действуют Пос­ледовательно и в одном и том же порядке. Поэтому можно записать, что

Теперь заметим, что умножение Тождественен перестановки

На любую другую перестановку S дает следующее:

Наконец, для каждой перестановки S можно найти ей Обратную, которая обозначается S–1 и действует так: если S переводит число K в число L, то S–1 переводит число L в число K. Например, для перестановки обратной будет перестановка . Из определения обратной перестановки немедленно вытекает, что

(6)

Если в равенствах (4)-(6) заменить символ о на + и вме­сто S–1 записать –S, то эти равенства совпадут с равенст­вами (3).

Ясно, что все сказанное относится и к подстановкам из любого числа элементов.

II. Следующий пример — геометрический. Мы будем рассматривать Множество всех движений на евклидовой плоскости Е. Движением называется всякая функция D, переводящая точки плоскости Е в точки той же плоскости Е, и сохраняющая длины отрезков. После­днее означает, что если D(A) = В, т. е. функция D пере­водит точку А в точку В, и D(C) = Е, то длина отрезка АС равна длине отрезка BE.

Отсюда, в частности, следует, что любое движение является взаимно однозначным преобразованием:* для всякой точки В существует единственная точка А, та­кая, что D(A) = В. Действительно, если бы движение D Переводило в точку В две различные точки А1 и A2, то отрезок нулевой длины ВВ перешел бы в отрезок A1A2, Имеющий ненулевую длину.

* Как, впрочем, и всякая подстановка.

К движениям относятся Параллельные переносы, повороты и симметрии.

Произвольный Параллельный перенос Т задается с помощью некоторого вектора . Вектор определяет в каждой точке А направленный отрезок АВ. Тогда по оп­ределению Т(А) = В. Следовательно, параллельных пе­реносов на плоскости столько же, сколько векторов.

Произвольный поворот R задается точкой С, около которой происходит вращение, и углом A, на который каждая точка плоскости поворачивается около точки С. Если точка А после поворота около точки С на угол A пе­решла в точку В, то по определению В(А) = В (рис. 37). Если поворот происходит против часовой стрелки, то угол A считается положительным, если по часовой стрелке — отрицательным. По определению R(С) = С.

Симметрия S (осевая симметрия) относительно некоторой прямой Р переводит точку А в точку В, сим­метричную относительно прямой Р, (см. рис. 37). Точки прямой Р функция S оставляет на своих местах.

Как и для подстановок, для любых двух движений D1 и D2 можно определить их композицию D1 D2 как результат последовательного действия:

.

При этом, в силу тех же обстоятельств, что и выше, для любых трех движений выполняется равенство

,

Аналогичное равенству (4).

Согласно определению, Тождественная функция I (I(А) = А) также является движением. Очевидно, что для нее выполняется равенство , аналогич­ное равенству (5).

Наконец, для каждого движения D существует ему обратное D–1, которое определяется естественным обра­зом: если D переводит точку А в точку В, то D–1 перево­дит точку B в точку А. Согласно этому определению, , т. е. выполняется равенство, анало­гичное равенству (6).

Можно доказать, что любое движение будет либо параллельным переносом, либо поворотом, либо симметри­ей, либо некоторой их композицией. Таким образом, мы описали Все движения.

Мы указали несколько важных математических объектов различной природы и выделили у них нечто общее, а именно

Каждый из объектов представляет собой некоторое множество, на котором задана операция (например, сложения, композиции и т. д.);

Свойства этой операции описываются аксиомами (3).

Такие множества называются Группами.

В соответствии с этим определением,

Множество целых, (рациональных, действительных) чисел является группой относительно операции сложения;

Множество рациональных (действительных) чисел Без нуля является группой относительно операции ум­ножения;

Множество всех подстановок из П элементов образует группу относительно операции композиции (умножения). В этой группе N! элементов, она называется Симметри­ческой группой и обозначается Sn;

Множество всех движений на евклидовой плоскости образует группу относительно операции композиции.

Мы рассмотрели лишь некоторые наиболее простые, но важные группы. Разумеется, есть и другие группы, причем их так много, что задача классификации групп не решена до сих пор.

Идея группы — одна из величайших идей в матема­тике. Она возникла в работе французского математика XIX в. Эвариста Галуа. К настоящему времени теория групп развита необычайно глубоко, и трудно указать та­кой раздел математики, где бы она ни принесла весомые результаты. Более того, группы хорошо работают, на­пример, в химии, кристаллографии, а современную фи­зику вообще невозможно представить без теории групп.

< Предыдущая		Следующая >