8.2. Векторы и векторные пространства
Рассматривая, как развивалось то или иное математическое понятие, мы учимся понимать роль и значение всей математики. Наряду с кольцами и полями, одним из важнейших понятий в математике, физике и технике является Вектор. Эволюция этого понятия — от Направленного отрезка до сложнейших Векторных пространств — история интересная и поучительная.
Первоначально вектором называли направленный отрезок, прикрепленный к какой-либо точке. С помощью направленных отрезков удобно иллюстрировать физические величины, которые характеризуются не только величиной, но и направлением: силу, скорость, напряженность электрического поля и т. д.
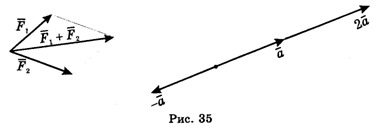
Векторы, прикрепленные к одной точке, можно складывать по правилу параллелограмма. С физической точки зрения сумма двух или более векторов представляет собой равнодействующую сил, действующих на точку (рис. 35).
Векторы, прикрепленные к одной точке, можно не только складывать, но и вычитать, умножать на числа. Разностью двух векторов ![]() и
и ![]() называется вектор
называется вектор ![]() —
— ![]() , Определяемый равенством
, Определяемый равенством ![]() + (
+ (![]() –
– ![]() ) =
) = ![]() . Произведением вектора
. Произведением вектора ![]() на число K называется вектор
на число K называется вектор ![]() = K
= K![]() , прикрепленный к той же точке, что и вектор
, прикрепленный к той же точке, что и вектор ![]() ; длина вектора
; длина вектора ![]() Определяется равенством |
Определяется равенством |![]() | = |K| • |
| = |K| • |![]() |, а направление совпадает с направлением вектора |
|, а направление совпадает с направлением вектора |![]() |, если K число положительное, и противоположно вектору
|, если K число положительное, и противоположно вектору ![]() , если K — Число отрицательное (рис. 35). При этом, каковы бы ни были векторы
, если K — Число отрицательное (рис. 35). При этом, каковы бы ни были векторы ![]() ,
, ![]() ,
, ![]() и числа K, I, всегда выполняются следующие равенства:
и числа K, I, всегда выполняются следующие равенства:
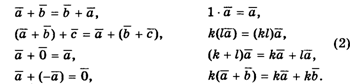
Математиков, которые рассматривают векторы вне их связи с физическим содержанием, не удовлетворяло, что нельзя складывать векторы, прикрепленные к разным точкам. Выход нашелся в том, чтобы сделать векторы свободными от точки прикрепления и разрешить им передвигаться параллельно исходному положению. Иными словами, Свободный вектор можно представлять себе в виде совокупности всевозможных направленных отрезков, параллельных между собой, имеющих одну и ту же длину и одно и то же направление. Такие отрезки называют Эквивалентными.
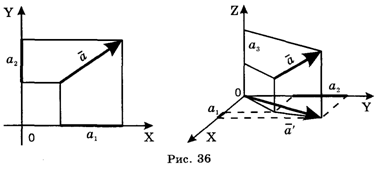
Свободные векторы просто задавать с помощью координат. Напомним, что Координатами вектора — направленного отрезка на плоскости называются его проекции на координатные оси Х и Y (см. рис. 36). Очевидно, что все эквивалентные направленные отрезки имеют одинаковые координаты. Поэтому последние можно считать координатами соответствующего свободного вектора.
В пространстве направленный отрезок имеет три координаты: проекции на координатные оси X, Y и Z. Следовательно, свободный вектор в пространстве имеет также три координаты.
Итак, теперь вектор можно заменить эквивалентным объектом — совокупностью его координат. Вектор на плоскости — это пара чисел (а1,а2), вектор в пространстве — тройка чисел (а1, а2, а3). Сложение векторов и умножение их на числа теперь осуществляется также просто. Чтобы сложить два вектора, нужно сложить их соответствующие координаты, а чтобы умножить вектор на число, нужно умножить на это число его координаты. Например, (1,2,–3) + (–4,6,4) = (–3,8,1), 2 • (1,2,–3) = (2,4,–6).
Такая точка зрения на векторы оказалась исключительно плодотворной. Под определение вектора сразу попало много физических и математических объектов. Например, всякое элементарное событие, происходящее в пространстве в точке с координатами (х, у,z) в момент времени T, можно рассматривать как четырехмерный вектор (X,Y,Z,T). Так мы приходим к Пространству событий — Одному из основных понятий современной физики. Другой пример. Всякий технологический процесс характеризуется набором различных параметров, которые фиксируются приборами, показывающими время, скорость процесса, давление, вязкость и т. п. Допустим, что таких параметров 10. Тогда состояние процесса определяется набором из десяти чисел, т. е. десятимерным вектором.
Количество координат вектора называется Размерностью. Векторы одной и той же размерности можно складывать и умножать на числа по тем же правилам, что двумерные и трехмерные. И при любой размерности будут выполняться свойства (2). Таким образом, мы приходим к наиболее общему аксиоматическому определению векторного пространства:
Векторным пространством называется всякое множество, для элементов которого определена операция сложения и определено умножение элементов на числа таким образом, что выполняются свойства (2).
Свободный вектор называют еще Параллельным векторным полем. Термин «векторное поле» возник в физике, и его смысл вполне соответствует значению этого слова в обычном языке. Мы представляем себе поле как некоторый участок земли, засеянный, скажем, пшеницей. Теперь представим себе, что колос пшеницы — это вектор, и что колосья (векторы) растут в каждой точке участка. Это и будет векторное поле, причем не обязательно параллельное. Параллельное поле получается в случае, когда все «колоски» параллельны и имеют одинаковую длину.
Множество примеров векторных полей мы находим в физике: электрические и магнитные поля, поле тяготения. Поток жидкости или газа в трубе порождает векторное поле скоростей: в каждой точке потока определен вектор скорости.
Математики иногда рассматривают векторное поле как функцию, которая каждой точке пространства сопоставляет некоторый вектор, как бы прикрепленный к этой точке. Векторные поля представляют собой один из важнейших объектов изучения в современной физике и математике.
| < Предыдущая | Следующая > |
|---|