8.1. Математические структуры. Кольца и поля

В основе математики лежит понятие множества. Множеством называют всякую совокупность каких-либо предметов.* Предметы, из которых состоит множество, называют его элементами. Если, например, в Твери 145 юристов, то можно сказать, что множество всех юристов города состоит из 145 элементов. Говорят о множестве студентов в аудитории, множестве ног тара­кана, множестве всех озер Тверской области, множестве книг в библиотеке и т. д.

* В то время как в русском языке слово «множество» означает «много».

В математике рассматриваются числовые множества, множества, состоящие из точек, прямых, векторов, мно­гочленов, функций. Они обозначаются специальными символами. Например, множества натуральных, целых, рациональных, вещественных и комплексных чисел (о последних см. наст. гл., §4) обозначают символами N, Z, Q, R и С соответственно.

Если элемент о принадлежит множеству М, то пи­шут А Î М. Например, 5 Î N, Î R. Если все элементы множества В принадлежат также множеству А, то говорят, что множество В является подмножеством множества А. Это записывается так: В Ì А. Говорят также «В содержится в А» или «В является частью А».

Множество, не содержащее ни одного элемента, называется Пустым, множеством и обозначается символом Æ. По определению считается, что пустое множество является подмножеством любого множества.

Математика, как и всякая другая наука, развивается путем постоянного обобщения и углубления уже имею­щихся результатов и фактов. Каждое очередное замеча­тельное открытие заставляет переосмысливать все на­копленное к этому моменту. Открытие неевклидовой геометрии, например, привело математиков к осознанию необходимости строгого обоснования основных матема­тических понятий, в том числе и тех, которыми они уже пользовались несколько столетий. Этот процесс на­чался примерно со второй половины XIX в. Одной из первых фундаментальных работ в этом направлении стало исследование аксиом геометрии, проведенное Да­видом Гильбертом, одним из величайших математиков конца XIX — первой половины XX в.

Идея Гильберта состояла в том, чтобы максимально формализовать основные математические определения. Под формализацией понимают замену интуитивного по­нятия строгим, смысл которого раскрывается в соответ­ствующей системе аксиом. Например, словами «точка» и «прямая» в системе аксиом евклидовой геометрии (см. гл. VIII, §2) обозначаются не обычные точки и прямые, с которыми мы привыкли иметь дело в школе и дома, а элементы каких-то абстрактных множеств, природа кото­рых нам безразлична, и от которых требуется только одно: чтобы они подчинялись заданной системе аксиом. С по­добными множествами мы уже имели дело, когда рас­сматривали модели геометрии Лобачевского. Там «пря­мыми» назывались хорды окружности (модель Клейна), лучи и полуокружности (модель Пуанкаре).

Помимо математической стройности ценность формального определения состоит еще и в том, что оно выяв­ляет общие свойства совершенно, казалось бы, различных математических объектов. Например, как мы отмечали в гл. I, числовые множества N, Z, Q, R имеют одинаковые алгебраические свойства: их элементы складывают, вычи­тают, умножают и делят по одним и тем же правилам:

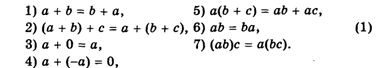
Но по этим же правилам производятся операции и с а) многочленами; б) со всеми элементарными функция­ми; в) с рядами (бесконечными суммами). Как мы уви­дим, есть и другие, более сложные множества, для ко­торых справедливы свойства (1). Таким образом, в свой­ствах (1) отражены некоторые общие свойства указан­ных множеств. Любое множество с такими свойствами называется Кольцом.*

* Точнее, коммутативным и ассоциативным кольцом.

Формальное определение кольца следующее: это не­которое множество, на котором заданы две функции, одна из которых называется Сложением, а вторая — Ум­ножением; сложение и умножение должны подчиняться правилам (1), которые называются Аксиомами кольца.*

* Свойства 6) и 7) иногда не включают в систему аксиом кольца.

Аксиомы 1), 2) и 5), 6), 7) представляют собой тож­дества, которые должны выполняться для любых эле­ментов А, B и С из кольца.

Аксиома 3) означает, что в кольце должен существо­вать особый элемент, называемый Нулем, для которого равенство 3) выполняется при любом А.

Аксиома 4) утверждает, что для каждого элемента А Из кольца найдется (в том же кольце!) Противоположный ему элемент –а, причем равенство 4) можно рас­сматривать как уравнение, из которого и определяется этот элемент –А.

УПРАЖНЕНИЯ

1. Покажите, что кольцом является а) множество чет­ных чисел; б) множество чисел, кратных трем; в) мно­жество чисел, кратных четырем, и т. д.

2. Будет ли кольцом множество всех положительных рациональных чисел?

В формальном определении кольца операции сложе­ния и умножения рассматриваются как функции. Такие функции в этом курсе нам еще не встречались. Здесь сумма А + b рассматривается как функция двух пере­менных А и B, т. е. слагаемых; произведение А • b — Также как функция двух переменных А и B, т. е. сомно­жителей. Таким образом, и независимые переменные (А и B) и значения этих функций (сумма и произведение) являются не числами, а Элементами кольца.

Как видно из системы аксиом (1), операция деления в кольце, вообще говоря, отсутствует. Кольца, в кото­рых можно делить на любой элемент, кроме нуля, на­зываются Полями. Формальное определение поля полу­чается добавлением к аксиомам (1) еще одной аксиомы, обеспечивающей возможность деления. Попробуйте сфор­мулировать ее самостоятельно.

В заключение рассмотрим еще два важных примера колец.

I. Докажем, что относительно обычных операций сложения и умножения числа вида А + B с рацио­нальными А и B образуют поле.

Обозначим рассматриваемое множество чисел через Р. Прежде всего нужно показать, что Множество Р замк­нуто относительно операций сложения и умножения, Т. е. что сложение и умножение можно рассматривать как функции со значениями во множестве Р. Иными слова­ми, нужно проверить, что сумма и произведение любых двух чисел из множества Р также принадлежат множе­ству Р, т. е. снова будут числами вида А + B.

Взяв пару чисел А + B и С + D, где А, B, с, D Î Q, Получаем:

Так как А, b, с, D — это рациональные числа (дроби), то и числа, которые получились в скобках, также будут дробями. Это мы и хотели показать.

Теперь докажем, что операция деления также не вы­водит нас из рассматриваемого множества. В самом деле,

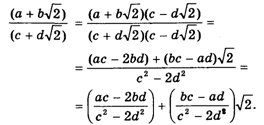
В скобках стоят рациональные числа, следовательно, результат деления двух любых чисел из множества Р Представляет собой число также из множества Р. Итак, числа вида А + b образуют поле, что и требовалось доказать.

Придумайте еще один похожий пример. Подумайте также, почему знаменатель С2 – 2D2 не равен нулю? От­вет можно найти в гл. I, §2.

II. Все целые числа разделим на шесть частей, кото­рые обозначим P0, Р1,..., P5 и будем называть Классами вычетов по модулю 6 или просто Классами.

По определению, класс Р0 состоит из чисел, кратных шести, т. е. 0, ±6, ±12, ±18, ... . Произвольное число из этого класса записывается в виде 6K, где K — произ­вольное целое число.

Класс P1 состоит из чисел, которые при делении на 6 дают в остатке единицу. Это числа.... –11, –5, 1, 7, 13, 19, .... Произвольное число из этого класса записывает­ся в виде 6K + 1.

Класс Р2 состоит из чисел, которые при делении на 6 дают в остатке два. Это числа..., –10, –4, 2, 8, 14, 20, ... . Произвольное число из этого класса записывается в виде 6K + 2.

И так далее. Наконец, класс P5 состоит из чисел, которые при делении на 6 дают в остатке пять. Это числа..., –7, –1, 5, 11, 17, 23, ... . Произвольное число из это­го класса записывается в виде 6K + 5.

Определим сложение классов формулой

Pk + Pl = Pk+L , если K + L < 6, и

Pk + Pl = Pk +L – 6 , если K + I ³ 6.

Например Р2 + P0 = P2 ,P3 + P4 =P1.

Используя тот же принцип, определим умножение классов. Положим PkPl = Рт, Где число Т есть остаток от деления числа Kl на шесть. Например, Р1Р4 = Р4, Р2Р5 = Р4, А РзP4 = P0 т. к. 3 • 4 = 12 делится на 6 без остатка.

Верно следующее утверждение:

Классы, вычетов по модулю шесть образуют кольцо относительно введенных операций сложения и умноже­ния, т. е. для них выполняются аксиомы кольца [см. (1)]:

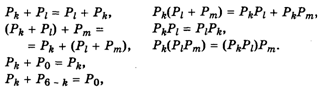
Доказательство этого утверждения состоит в проверке всех аксиом. Так как оно несложное, мы не приводим его, а предлагаем читателю сделать это самостоятельно.

Итак, мы построили кольцо всего из шести элементов (оно обозначается Z6), в то время как все перечисленные ранее кольца — числовые, кольцо многочленов и т. д., содержат Бесконечно много элементов. Аналогичным об­разом можно построить кольцо Zm классов вычетов по любому модулю Т, содержащее всего Т элементов.

Возникает естественный вопрос: являются ли кольца вычетов полями? Иными словами, можно ли ввести операцию деления классов? Попробуем, например, раз­делить P2 На P3 кольце Z6. Пусть P2 : P3 = РX, Тогда P2 = Р3РX. Но, согласно определению,

Итак, при любом Х имеем Р3Рх ¹ P2 , а этo и означа­ет, что частного P2 : Р3 не существует. Следовательно, кольцо Z6 не является полем.

С другой стороны, таким же способом можно пока­зать, что, например, кольца Z3, Z5 и Z7 будут полями. Общий результат формулируется так: кольцо Zm является полем тогда и только тогда, когда Т — простое число.

Кольца и поля вычетов играют в математике важную роль, особенно в теории чисел. С их помощью, напри­мер, находят Целочисленные решения (Х, у) уравнений вида Ax + By = с, коэффициентами которых являются также целые числа.

< Предыдущая		Следующая >