7.3. От Евклида до Лобачевского (история неевклидовой геометрии)

Вокруг изобретателей новых цен­ностей вращается мир — неслышно вращается он.

Ф. Ницше. «Так говорил Заращустра»

История неевклидовой геометрии — самый замечательный пример развития Математической Идеи. Для нас эта история интересна вдвойне, т. к. ее главный участ­ник — гениальный русский математик Николай Ивано­вич Лобачевский.

А началась эта история примерно 2300 лет назад, когда греческий математик Евклид написал книгу под названием «Начала». В ней он систематизировал все имевшиеся к тому времени сведения по геометрии и из­ложил их с таким непревзойденным педагогическим мастерством, что на протяжении тысячелетий «Начала» были лучшим учебником по геометрии.*

* Не устарела эта книга и сейчас. По существу, все современ­ные школьные учебники идейно и структурно копируют «Начала».

Каким же образом Евклид сумел изложить геомет­рию так просто и с таким изяществом, что покорил целые поколения, а по числу изданий и читаемости его книга сравнима только с Библией?

Евклид предложил метод, который теперь называет­ся Аксиоматическим и широко применяется в математике и других науках. Суть его состоит в том, что при изложении некоторой теории в самом начале формули­руется ряд утверждений, называемых Аксиомами, ис­тинность которых считается несомненной. (Про такие утверждения еще говорят, что они «принимаются без доказательства».)

Аксиомы должны быть достаточно простыми и соответствовать нашему опыту. А дальнейшее развитие теории состоит в доказательстве теорем, вытекающих толь­ко из заданных аксиом.

Система аксиом Евклида на протяжении более 2000 лет совершенствовалась многими авторами. В настоящее время существует много различных редакций системы аксиом евклидовой геометрии. Вот одна из них.

Аксиомы евклидовой геометрии на плоскости

Первая группа: аксиомы связи

1. Через две различные точки проходит одна и толь­ко одна прямая.

2. На каждой прямой имеются по крайней мере две различные точки.

3. Существуют три точки, не лежащие на одной прямой.

Вторая группа: аксиомы порядка

1. Если точка В лежит между точками А и С, то В лежит между С и А.

2. Из трех различных точек на прямой одна и толь­ко одна лежит между двумя другими.

3. Всякая прямая разбивает плоскость на две части таким образом, что для любого отрезка на плоскости выполняется следующее: если концы отрезка принад­лежат одной и той же части, то прямая не пересекает этот отрезок; если же концы отрезка принадлежат раз­ным частям, то прямая его пересекает.

Третья группа: аксиомы движения

1. Каждое движение сохраняет принадлежность точ­ки прямой.

2. Каждое движение сохраняет порядок точек на прямой.

3. Композиция двух движений также является движением.

4. Для каждого движения существует обратное движение.

5. Если некоторое движение оставляет на месте луч и его начало, то оно оставляет на месте каждую точку этого луча.

6. Какую бы пару точек мы ни взяли, существует движение, которое переставляет их местами.

7. Какую бы пару лучей с общим началом мы ни взяли, существует движение, которое переставляет их местами.

Четвертая группа: аксиома непрерывности (Дедекинда)

Пусть все точки прямой разбиты на два непустых класса так, что каждая точка первого класса предше­ствует каждой точке второго класса. Тогда либо в пер­вом классе существует точка, следующая за всеми ос­тальными точками первого класса, либо во втором клас­се существует точка, предшествующая всем точкам вто­рого класса.

Пятая группа: аксиома параллельности (пятый пос­тулат Евклида)

На плоскости через точку М, не лежащую на прямой А, можно провести одну и только одну прямую, парал­лельную прямой А.

Аксиома параллельности — самое знаменитое математическое предложение в истории. Ее обсуждение на протяжении 2000 лет завершилось гениальным откры­тием Лобачевского и привело к открытию неевклидовых геометрий, возникновению новых областей в математи­ке и новым взглядам на пространство и время.

Почему же так получилось? Дело в том, что, начи­ная со времен Евклида, многие математики не воспринимали аксиому параллельности именно как аксиому, а стремились ее доказать, потому что она казалась слож­нее остальных аксиом. Позже появился другой мотив. Утверждение, содержащееся в пятом постулате, стало казаться настолько соответствующим действительности и человеческому опыту, что никто из математиков до Лобачевского (кроме великого Гаусса) не сомневался в существовании доказательства.

За 2000 лет было предложено очень много «доказательств», но все они имели один и тот же порок: каж­дый автор, сам того не замечая, обязательно использо­вал в своих рассуждениях ту самую аксиому параллель­ности, которую стремился доказать! В математике это называется порочным кругом. Ясно, что подобные рассуждения доказательством не являются.

Николай Лобачевский, как и многие его предшественники и современники, тоже увлекся доказатель­ством пятого постулата. После нескольких неудачных попыток он решил применить доказательство «от про­тивного». Для этого Лобачевский заменил аксиому параллельности Евклида на противоположную:

На плоскости через точку М, не лежащую на прямой а, проходит более одной прямой, параллельной данной прямой а,

Оставив остальные аксиомы Евклида без изменения. За­тем он стал доказывать с помощью новой системы акси­ом различные теоремы в надежде получить противоре­чие. Если бы на некотором этапе рассуждений таковое оказалось, то это означало бы, что аксиома параллель­ности Лобачевского неверна, а следовательно, верна толь­ко аксиома Евклида. Но, доказав несколько десятков теорем, Лобачевский никакого противоречия не получил. И тогда он понял, что с математической точки зрения его система аксиом имеет такое же право на существование как и система аксиом Евклида. Так родилась неевклидова геометрия. Датой рождения считается 1826 год, когда Лобачевский доложил результаты своих исследо­ваний на заседании математического факультета Казан­ского университета.

Изменение всего лишь одной аксиомы привело к удивительным фактам. В новой, неевклидовой геометрии

Сумма углов любого треугольника оказалась меньше 180°, причем эта сумма зависела от площади S треугольника:

.

Здесь K — некоторая постоянная, определяемая выбором масштаба. Из этой формулы видно, что площадь любого треугольника не может быть более K2.

Далее, оказалось, что в геометрии Лобачевского нет подобных фигур! Например, получалась такая теорема: если у двух треугольников углы равны, то эти треуголь­ники равны. Этот удивительный факт объясняется тем, что теория подобия основана на понятии параллельности. Отменяя аксиому параллельности Евклида, мы отменя­ем и подобие.

Кроме параллельных и пересекающихся прямых, на плоскости Лобачевского существуют Расходящиеся или Сверхпараллельные прямые; помимо обычных окружно­стей, есть окружности, центр которых находится в бес­конечности, и т. д.

Лобачевский понимал, что, открыв новую геомет­рию, он должен найти ответ на некоторые вопросы. Важнейший из них такой: как новая геометрия соотно­сится с реальным миром? Лобачевский был убежден, что его геометрия — не абстрактная математическая теория, не только плод его ума, а что она отражает свойства реального пространства. Он считал, что во Все­ленной действует именно его геометрия, но люди этого не замечают, т. к. различие между евклидовой и новой геометрией проявляется только при измерении очень больших расстояний. Если же измерять небольшие фи­гуры, то результаты, полученные с помощью формул старой и новой геометрии, отличаются настолько мало, что это различие заметить практически невозможно. Точнее: чем меньше измеряемые фигуры, тем геометрия Лобачевского ближе к геометрии Евклида.

Чтобы проверить эту гипотезу, Лобачевский решил найти сумму углов треугольника, две вершины которого находятся в противоположных концах земной орбиты, а третья — на звезде Сириус. Если бы сумма углов оказа­лась меньше 180°, то гипотеза Лобачевского получила бы подтверждение.

Проведя предварительные вычисления, Лобачевский установил, что если сумма углов в этом треугольнике и окажется меньше чем 180°, то не более чем на 4 милли­онных секунды! (Секунда — 1/3600 часть градуса.) По­этому практические измерения выполнить невозможно, т. к. ни один из астрономических приборов не обладал (и до сих пор не обладает) требуемой точностью.

Другая важная проблема заключалась в необходимо­сти выяснить, не содержит ли система аксиом новой геометрии каких-либо внутренних противоречий? Ведь никто не может доказать Все теоремы, поэтому нужно как-то гарантировать, что пользуясь аксиомами, мы ни­когда не получим взаимоисключающих результатов. Лобачевский много работал над этой проблемой, но она оказалась настолько глубокой и сложной, что завершить ее удалось только через несколько десятилетий усилия­ми многих замечательных математиков.

Новая геометрия не получила признания при жизни ее творца. Она получила известность только после 1868 г., когда появилась ее первая Модель. Модель не­которой геометрии представляет собой совокупность ма­тематических объектов, называемых «точками» и «прямыми», для которых выполняются аксиомы этой геометрии.

Модель евклидовой геометрии построить очень про­сто, для этого достаточно вспомнить, что такое декарто­вы координаты на плоскости. Назовем «точкой» всякую упорядоченную пару чисел (х, у), а «прямой» — множе­ство точек, координаты которых удовлетворяют уравне­нию вида Ax + By + С = 0. Можно проверить, что для таких «прямых» и «точек» выполняются все перечис­ленные выше аксиомы евклидовой геометрии.

Модель Клейна плоско­сти Лобачевского строится внутри некоторого круга К. «Точками» называются обычные точки, находящи­еся внутри круга К, а пря­мыми — хорды окружнос­ти S, ограничивающей круг К (см. рис. 33). Параллельные прямые изображаются хордами, пересекающимися на окружности S; непересекающиеся хорды — это сверх­параллельные (расходящиеся) прямые. Можно показать, что на этой модели выполняются все аксиомы геометрии Лобачевского, т. е. все, кроме последней, аксиомы евкли­довой геометрии и сформулированная выше аксиома па­раллельности Лобачевского.

Расстояние (в смысле геометрии Лобачевского) между точками A И В вычисляется по следующей формуле

Аналогичную формулу можно записать и для углов.

В другой модели (Пуанкаре) «точками» плоскости Лобачевского будут точки верхней полуплоскости (Х > 0), прямыми — лучи, перпендикулярные оси X, а также полуокружности, опирающиеся на ось Х (см. рис. 34).

Расстояние (в смысле геометрии Лобачевского) между точками А и В вычисляется по формуле

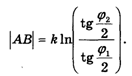
Для вычисления углов специальная формула не нужна: на модели Пуанкаре углы в смысле геометрии Лобачев­ского — это обычные углы.

Есть и другие модели геометрии Лобачевского.

Существование моделей доказывает, что система ак­сиом Лобачевского является Непротиворечивой. Так решается одна из важнейших проблем, над которой в последние годы жизни работал сам Лобачевский.

С другой стороны, наличие моделей, или как еще говорят, Реализации геометрий Евклида и Лобачевского, закрывает проблему 2000-летней давности: можно ли Доказать аксиому параллельности, т. е. вывести ее из других аксиом? Теперь ясно, что нельзя, потому что эта аксиома Не зависит от остальных аксиом. Независи­мость вытекает из того факта, что после замены аксио­мы параллельности Евклида на аксиому параллельности Лобачевского мы вновь получаем непротиворечивую си­стему аксиом.

Переоценить значение открытия Лобачевского не­возможно. Никакой другой математический результат не имел столько значительных последствий. Благодаря открытию геометрии Лобачевского возникли новые важнейшие области математики: основания геометрии, основания математики, математическая логика. Мате­матики поняли силу аксиоматического метода и стали его широко применять во всех разделах математики и даже в физике. Далее, поскольку возник новый матема­тический объект — система аксиом — появились и спе­циальные методы его исследования, так называемая ме­таматематика. Бурно развилась теория алгоритмов, тесно связанная с математическими основами функциони­рования электронно-вычислительных устройств. В итоге было подвергнуто анализу все здание математики.

Идея Лобачевского, что наш мир только в «малом» подчиняется законам евклидовой геометрии, а в целом является неевклидовым, стала доминирующей идеей в науке с конца XIX века. Один из основных выводов те­ории относительности как раз и заключается в том, что пространство искривлено, т. е. не является евклидовым.

История пятого постулата показывает, как конкретная математическая идея, пройдя тысячелетия, как бы связала различные эпохи и стала одним из тех стержней, около которых вращается мир. Гениальные умы и великие мас­тера вращают наш мир, создавая настоящие ценности, и среди них математика — одна из звезд первой величины.

Ни одно из замечательных открытий в математике не остается без приложений. Совершенную теорию ко­нических сечений* создал еще греческий математик Аполлоний за 200 лет до н. э. Первое же практическое приложение этой теории было дано только в начале XVII в. величайшим астрономом Кеплером, который сформулировал один из своих законов так: Все планеты движутся по эллиптическим орбитам, в одном из фо­кусов которых находится Солнце.**

* Это эллипсы, гиперболы и параболы, которые получаются как линии пересечения кругового конуса с различными плоскостями.

** Напомним, что Эллипсом называется кривая, все точки которой обладают одним и тем же свойством: сумма расстояний от каждой точки эллипса до двух фиксированных точек, на­зываемых фокусами, есть величина постоянная, т. е. одна и та же для всех точек эллипса.

Таким образом, теория конических сечений ждала своего приложения 1800 лет.

Когда Лобачевский открыл свою геометрию, многие его современники, в том числе даже такой выдающийся математик, как Остроградский, считали неевклидову геометрию не более чем подозрительной забавой. Но уже через 50 лет появилось много неевклидовых геометрий, а через 75 лет Эйнштейн сформулировал принципы тео­рии относительности, и с этого момента неевклидовы геометрии стали рабочим инструментом физиков.

Еще меньше времени прошло от рождения матема­тической логики, которая вначале считалась сугубо формальной наукой, до того момента, когда вдруг выяс­нилось, что развитые ею методы — основа для создания будущих ЭВМ.

И таких примеров немало. Все они показывают, что на великом дереве математики зреет может быть и не так много плодов, но каждый из них, созрев, продвига­ет человечество на шаг вперед.

< Предыдущая		Следующая >