8.5. Алгебры Буля
Алгебры Буля названы так по имени открывшего их математика Джона Буля (середина XIX в.). Их эффективно применяют в математической логике, теории вероятностей и других разделах математики; с их помощью описывают работу различных управляющих систем — релейно-контактных и электронных схем, логических сетей, схем функциональных элементов и т. п.; используют в математической кибернетике — науке об управлении, созданной в середине XX в. Норбертом Винером.
Рассмотрим некоторые простые задачи, приводящие к алгебрам Буля.

Пример 1. На автомобильной дороге есть 3 опасных участка, А, В и С, которые после дождя могут стать непроходимыми (рис. 38). Кроме того, в тех местах часто бывают густые туманы и другие неприятности. Эти участки можно обойти по другой дороге, но и там есть столь же опасные участки D и Е.
Сведения о состоянии указанных участков систематически поступают к дежурному ГАИ, который в любой момент должен быть готов ответить на вопрос: можно проехать по трассе или нет? Задача состоит в том, чтобы сконструировать логическое устройство, которое поможет быстро дать правильный ответ.
Обозначим через А сообщение о состоянии участка А, через В — сообщение о состоянии участка В и т. д. Сообщения могут быть двух типов (принимают два значения): И — дорога в нормальном состоянии и Л — дорога непроходима. Пусть произведение АВ обозначает сообщение, которое характеризует состояние дороги на обоих участках А и В. Если участки А и В проходимы, то проходим и суммарный участок XY (см. рис. 39). Поэтому АВ принимает значение И только в том случае, когда оба сообщения, А И B, принимают значение И. Во всех остальных случаях сообщение АВ принимает значение Л. Короче говоря, мы можем определить произведение АВ с помощью следующей таблицы:

Таким образом мы ввели понятие Произведения двух сообщений.
Далее, от Y до Z можно добраться двумя путями, через участок С или участок Е. Поэтому вопрос, который нас интересует, можно сформулировать так: можно ли проехать Хотя бы по одному из этих участков? Пусть сумма С + Е обозначает некоторое сообщение, которое характеризует возможность проезда от Y до Z. Именно, С + Е принимает значение И (путь открыт!) в том случае, когда пригоден для проезда хотя бы один из участков С или D, т. е. одно из сообщений С или Е принимает значение И). Итак, мы определяем сумму С + Е следующей таблицей:

Используя эти понятия, мы можем теперь записать сообщение S, которое принимает значение И, если проезд от Х до Z возможен, и значение Л в противном случае. Оно имеет вид:
S=(AB+ D)(C + E). (10)
Допустим, дежурный получил сообщения, имеющие соответствующие значения:
![]()
Подставив их в формулу (10), он с помощью таблиц (8) и (9) вычислил значение сообщения S: (ИЛ + И) ´ (Л + И) = (Л + И)И = ИИ = И. Путь открыт.
На самом деле, дежурному вовсе не обязательно все время пользоваться формулой (10). Легко реализовать простейшее техническое приспособление, которое будет работать автоматически. Представьте себе, что на рис. 38 изображена электрическая цепь, которая может быть разомкнута на участках А, В, С, D, E. В обычном режиме цепь замкнута, по ней идет ток и в конечной точке Z горит лампочка. Это означает, что проезд возможен.
В случае, если, например, с участка А приходит сигнал Л (участок непроходим), то автоматически размыкается электрическая цепь на участке А. Но лампочка продолжает гореть, т. к. в цепи есть ток (проезд еще возможен). Как только лампочка погасла — проезда нет.
Мы привели простой пример. В рассматриваемой ситуации дежурный вполне мог обойтись и без столь глубокого логического анализа. Однако подобный анализ совершенно необходим, если мы намереваемся управлять сложными системами, например, дорожной сетью большого города.
Математическую основу наших рассуждений составляют таблицы (8) и (9). Они определяют операции умножения и сложения на множестве объектов А, В, С, ..., Каждый из которых может принимать два значения — И или Л. Такие множества (вместе с указанными операциями) называются Алгебрами Буля. Точное определение алгебры Буля таково: 1) это множество элементов А, В, С, ..., каждый из которых может принимать два значения И или Л; 2) элементы можно умножать и складывать по формулам (8) и (9); 3) для каждого элемента А найдется такой элемент ![]() , который принимает противоположное значение:
, который принимает противоположное значение:
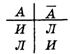
Приведем еще некоторые примеры алгебр Буля. Случайные события, рассмотренные в гл. IV, образуют алгебру Буля относительно введенных для них операций сложения и умножения. В математической логике рассматриваются алгебры Буля, элементами которых являются Высказывания. Каждое высказывание может быть либо истинным (т. е. принимать значение И), либо ложным (т. е. принимать значение Л). Высказывание, противоположное высказыванию А, обозначается через ![]() .*
.*
* Совокупность всех подмножеств данного множества образует алгебру Буля относительно операций объединения и пересечения множеств.
Пример 2. Во время допроса каждый из четырех подозреваемых сделал следователю три заявления.
Валет: я не виновен; Туза я не знаю; Серый знает, кто это сделал.
Хват: это сделал не я; с Серым я не знаком; это сделал Туз.
Туз: я не виновен; это сделал Серый; Хват лжет, это сделал не я.
Серый: я не виновен; это сделал Валет; Хват может за меня поручиться.
При перекрестном допросе каждый из подозреваемых признал, что из трех сделанных им заявлений два верных и одно неверное. Может ли следователь определить преступника на основании полученной информации?
Проанализируем высказывания, сделанные в ходе допроса. Для этого формализуем наши рассуждения.
Обозначим высказывания подозреваемых В1, B2, B3, Х1, Х2, Х3 и т. д. Наша цель — установить, какие из них являются истинными, а какие — ложными. Запись Х1 = И, например, будет далее обозначать, что первое высказывание Хвата истинно.
Прежде всего заметим, что первое и третье высказывания Туза логически связаны между собой и, по существу, представляют собой одно и то же утверждение «я не виноват». Поэтому они либо оба истинны, либо оба ложны. Но т. к. из трех высказываний Туза ложное только одно, то остается единственный вариант: оба высказывания, первое и третье, являются истинными. Следовательно, можно записать Т1 = И, Т2 = Л, Т3 = И.
Теперь ясно, что третье высказывание Хвата (преступник — Туз) является ложным. Поэтому остальные два истинны. Итак, X1 = И, Х2 = И, Х3 = Л.
Поскольку высказывание Т2 ложно, то Серый не виновен. Значит, C1 = И. Кроме того, высказывание С3 ложно, т. к. истинно Х2. Следовательно, C2 = И. Но это означает, что преступник — Валет, т. е. В1 = Л, В2 = И, В3 = И.
По существу, подобный логический анализ проводит всякий опытный следователь. Однако в реальных делах часто бывает весьма большое число участников (свидетелей, подозреваемых и т. д.); следовательно, приходится анализировать большое число высказываний. В таких случаях результаты представляют в виде таблиц, диаграмм, схем и т. п. Так, результаты наших рассуждений можно оформить в следующей таблице:
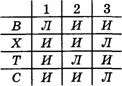
Мы последовательно заполняли третью, вторую, четвертую и первую строки.
Для анализа большого числа данных обычно используют компьютеры, которые способны перебрать практически любое число вариантов. Процедура перебора осуществляется с помощью формул алгебры Буля. Для каждого из вариантов машина проверяет, выполняются ли заданные связи между высказываниями, которые записываются на языке алгебры Буля. В рассмотренной нами задаче число различных вариантов заполнения таблицы равно 81 (докажите это, используя правило умножения из гл. III), а связи между высказываниями таковы:
T1 = T3 , X3 = ![]() ,
, ![]() = C1 ,C2 =
= C1 ,C2 = ![]() .
.
(Напомним, что через ![]() обозначается высказывание, противоположное высказыванию А.)
обозначается высказывание, противоположное высказыванию А.)
В заключение отметим, что, с одной стороны, алгебры Буля представляют собой теоретическую (логическую) основу для расчета различных электронно-вычислительных схем, т. к. любая электрическая цепь может находиться в одном из двух состояний: либо она пропускает ток, либо нет. Это и позволяет считать цепи элементами алгебры Буля со значениями И или Л. С другой стороны, с помощью ЭВМ можно эффективно анализировать различные ситуации, подобные описанным выше.
| < Предыдущая | Следующая > |
|---|