6.3. Интеграл
Одна из самых распространенных практических задач — вычисление длин, площадей, объемов и т. д. Если фигура простая (отрезок прямой, окружность, треугольник, параллелограмм, правильная пирамида и т. д.), то можно воспользоваться простейшими формулами, которые были известны еще математикам древности. В случае же, если фигура достаточно сложная, простыми формулами уже не обойтись. Тогда применяют Интегральное исчисление.
Различают Определенный и Неопределенный интегралы. Любой из вас, прочитавший предыдущий параграф и уже научившийся находить производную от заданной функции, несомненно спросил себя: а как найти функцию, если известна ее производная? Процедура нахождения производной по заданной функции называется Дифференцированием, а обратная процедура, позволяющая находить по заданной производной исходную функцию, называется Интегрированием. Результат интегрирования называется Первообразной функцией. Так как производная от постоянной равна нулю, то
(F(X) + с)' = F'(X),
Где С — любое действительное число. Поэтому, если для заданной функции F(X) существует одна первоообразная F(X), то их существует бесконечно много: F(X) + с. Совокупность всех первообразных заданной функции F(X) Называется Неопределенным интегралом и для его записи используют весьма специфическое обозначение:
![]()
Например,
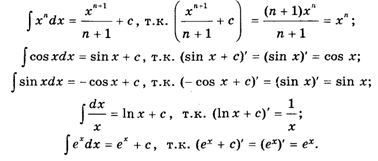
Присутствующая всюду постоянная с называется Постоянной интегрирования.
К понятию определенного интеграла мы приходим при вычислении длины, площади, объема и т. д. Проиллюстрируем это на простейшем случае — вычислении площади под кривой.
Пусть У = F(X) — некоторая непрерывная функция (см. гл. VI, §1), заданная на промежутке [а, b]. Обозначим через S площадь между графиком этой функции и осью Х (рис. 32).
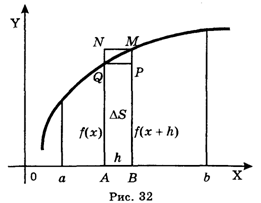
Чтобы найти S, разобьем отрезок [а,B] на маленькие равные отрезки длиной H и обозначим через DS ту часть искомой площади, которая находится над отрезком АВ (на рисунке она заштрихована). На рисунке видно, что верхняя граница заштрихованной фигуры находится между отрезками MN и PQ, которые ограничивают прямоугольники ABMN и ABPQ. Поэтому площадь заштрихованной фигуры заключена между площадями этих прямоугольников:
![]()
Так как AQ = F(X), ВМ = F(X + H), то SABPQ = F(X)H, SABMN = F(X + H)H и предыдущие неравенства принимают вид
![]()
Аналогичные неравенства запишем для каждого из отрезков длины H, на которые разбит отрезок [а,B], а затем все такие неравенства сложим. В результате получим неравенства
![]()
Где через S обозначена сумма всех фигур типа SABPN, Т. е. искомая площадь; буквой S1 обозначена суммарная площадь всех прямоугольников типа ABPQ, а через S2 — общая площадь всех прямоугольников типа ABMN.
Величины S1 и S2 являются функциями от переменной H. Если H неограниченно уменьшать (h ® 0), то S1 и S2 будут меняться, причем S2 будет уменьшаться, а S1 — увеличиваться. Обе суммы имеют своим общим пределом число S — площадь рассматриваемой фигуры.
Итак, площадь получается как предел ![]() (или
(или ![]() , который называется Определенным интегралом И обозначается
, который называется Определенным интегралом И обозначается
![]()
Связь между неопределенным и определенным интегралами устанавливается формулой Ньютона—Лейбница:
![]()
Где через F(X) обозначена первообразная функции F(X). Этой формулой и заканчивается процедура вычисления площади.
Примеры.
1. Найдем площадь под параболой Y = x2, 0 £ X £ l. Здесь А = 0, B = 1, поэтому
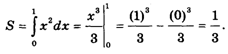
2. Найдем площадь под гиперболой У = ![]() , 1 £ X £ 2.
, 1 £ X £ 2.
Имеем:
![]()
3. Найдем площадь под графиком экспоненты У = ex, х £ 0. Имеем:
![]()
В заключение приведем пример неэлементарной функции, которая имеет важные и многочисленные приложения.
Во второй главе мы рассматривали Случайные величины, т. е. такие переменные величины, значения которых зависят от случая. Например, число дорожных происшествий на улицах города в течение суток; число новорожденных за месяц; число заявлений, поступивших в отделение милиции; скорость молекулы газа при определенной температуре; число метеоритов, падающих на Землю, и т. д. Сейчас мы рассмотрим еще одну величину, которая называется Случайной ошибкой.
Пример
4. В течение часа проведено 10 измерений уровня радиации одним и тем же прибором (в микрорентгенах в час): 12,0 11,5 11,7 12,2 12,1 10,8 11,6 10,7 12,0 11,4. Результаты измерений получились различными вследствие того, что и сам прибор, и человеческий глаз не являются идеальными орудиями наблюдения. Погрешность не может быть меньше толщины стрелки прибора; стрелка может вибрировать; угол, под которым мы смотрим на стрелку, также меняется. Кроме того, влияние оказывают атмосферные условия, настроение наблюдателя и т. п. Конечно, мы считаем, что исключены всякого рода систематические ошибки, связанные, например, с неисправностью прибора.
В отчете обычно показывают среднее арифметическое всех наблюдений. В нашем примере
![]() =
= ![]() (12 + 11,5 + 11,7 + 12,2 + 12,1 + 10,8 + 10 + 11,6 + 10,7 +12 + 11,4 + 11,6) = 11,6.
(12 + 11,5 + 11,7 + 12,2 + 12,1 + 10,8 + 10 + 11,6 + 10,7 +12 + 11,4 + 11,6) = 11,6.
Но для решения многих экологических проблем важно уметь оценить, насколько найденное среднее отличается от истинного значения радиации, которое нам неизвестно (ведь в нашем распоряжении имеются только показания приборов!). Как быть?
К счастью, математики умеют отвечать на этот вопрос. Назовем Случайной ошибкой разность между средним значением ![]() И истинным значением радиации. Так как истинное значение нам неизвестно, то и случайная ошибка тоже неизвестна. Многолетние наблюдения в различных экспериментах показали, что если число опытов достаточно велико, то случайные ошибки подчиняются некоторым общим закономерностям. Для их описания используется, как правило, так называемая интегральная функция Лапласа:
И истинным значением радиации. Так как истинное значение нам неизвестно, то и случайная ошибка тоже неизвестна. Многолетние наблюдения в различных экспериментах показали, что если число опытов достаточно велико, то случайные ошибки подчиняются некоторым общим закономерностям. Для их описания используется, как правило, так называемая интегральная функция Лапласа:
![]()
Этот интеграл не выражается через элементарные функции. Но его приближенные значения табулированы (см. Приложение на с. 219).
С помощью таблицы значений функции Ф(A) легко вычислить, например, вероятность того, что случайная ошибка не превосходит заданной величины H. Обозначим через P(H) вероятность того, что истинное значение наблюдаемой величины отличается от найденного среднего значения ![]() Не более чем на H. Величину P(H) находят по следующей формуле:
Не более чем на H. Величину P(H) находят по следующей формуле:
![]()
Здесь N — число измерений, a S — среднее квадратическое отклонение полученных значений. В нашем примере N = 10,
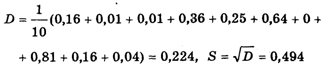
[см. гл. II, формулы (5), (7)]. Пусть H = 0,3, тогда
![]()
Пользуясь теперь формулой (7) и Приложением, находим:
![]()
Таким образом, с вероятностью 0,93 истинное значение величины радиации заключено в промежутке от 11,6 – 0,3 = 11,3 до 11,6 + 0,3 = 11,9.
Как понимать полученный результат? Допустим, что радиационный фон в данной местности измеряли параллельно несколько бригад. Их результаты будут, вообще говоря, различными: у каждой бригады получится свое среднее значение ![]() . Можно гарантировать, что примерно 93% найденных средних отклоняется от истинного значения не более чем на 0,3.
. Можно гарантировать, что примерно 93% найденных средних отклоняется от истинного значения не более чем на 0,3.
ТИПОВОЕ ЗАДАНИЕ
Проводится измерение уровня загрязненности атмосферы в центре города. Получены следующие значения индекса загрязнения:
27 29 23 30 31 25 30 29 24 29 31 28 28 24 29 26 30 29 28 25 28 30 29 27 25 28 27 32 31 28.
Найдите среднее значение индекса загрязнения и вероятность того, что оно отличается от истинного значения меньше, чем на 2.
| < Предыдущая | Следующая > |
|---|