6.2. Производная
Наиболее естественно к понятию производной мы приходим из кинематических соображений.
Напомним, что скорость тела, движущегося равномерно и прямолинейно, вычисляется по формуле
![]() .
.
Если тело движется прямолинейно, но не равномерно, то скорость в каждый момент времени, вообще говоря, разная. Скорость тела в момент времени T называют Мгновенной скоростью в точке T и обозначают V(T).
Предположим теперь, что к моменту времени T тело прошло путь S(T), а к моменту времени T + H (т. е. еще через промежуток времени H) — путь S(T + h). Тогда за время H оно прошло путь S(T + H) – S(T) и средняя скорость на этом участке будет
![]() .
.
Предположим теперь, что промежуток H уменьшается и стремится к нулю. Тогда и путь, пройденный за это время, также стремится к нулю, а средняя скорость Vcp За промежуток времени H стремится к скорости тела в момент T. Используя определение предела, можно записать:
![]() .
.
Эта формула является строгим определением мгновенной скорости и одновременно дает способ для ее вычисления. Предел V(T) существует при естественном допущении, что в момент времени T не было никаких катаклизмов: поезд не сошел с рельсов, не было столкновения или резкого торможения, не изменился внезапно коэффициент трения, поезд не утащила летающая тарелка и т. п.
Пример 1. При равномерном движении пройденный путь пропорционален времени, т. е. S(T) = Ct, где С — постоянное число. Используя предыдущую формулу, вычислим мгновенную скорость в момент времени T:
![]()
Формула для пути теперь запишется известным образом:
S = Vt.
Пример 2. До Галилея считалось, что все тела падают с постоянной скоростью. Проверить это на практике было сложно. Галилей высказал предположение, что все тела падают равноускоренно, т. е. при свободном падении путь пропорционален квадрату времени:
S = Ct2.
Найдем скорость в момент времени T:
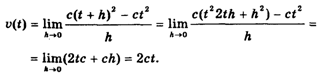
В случае свободного падения тела величина 2С найдена опытным путем. Она называется ускорением свободного падения и обозначается буквой G. Приближенно ![]() .
.
Теперь откажемся от физической терминологии и перейдем к стандартным обозначениям. Вместо «путь S(T)» будем говорить «функция F(X)», а вместо «скорость» говорить «Производная функции F(X) в точке х». Будем записывать функцию, как обычно, У = F(X), a производную этой функции в точке Х будем обозначать ![]() . Итак, по определению,
. Итак, по определению,
![]()
А из примеров 1 и 2 получаем:
![]()
Найдем производные от некоторых известных функций.
0. Производная от постоянной функции равна нулю, т. к., если функция не меняется, то ее приращение равно нулю: F(X + H) – F(X) = 0.
1. Производная от степенной функции У = Xп, N Î N. Согласно определению производной
![]()
По формуле бинома Ньютона (см. §1)
![]()
Вычтем отсюда XN, поделим почленно на H и запишем предел суммы как сумму пределов:
![]()
Все пределы, кроме первого, равны нулю, поэтому остается только
![]()
Это правило применимо и для отрицательных степеней:
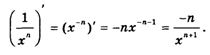
2. Производная от синуса.
Пользуясь определением производной, известной тригонометрической формулой «разность синусов» и свойствами предела, получаем:
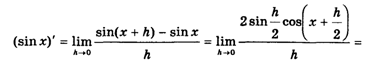
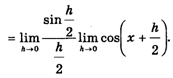
Первый предел равен единице (первый замечательный предел). Второй, используя непрерывность косинуса (см. с. 113), найдем так:
![]()
Итак,
![]()
Аналогично доказывается, что
![]()
3. Производная от показательной функции У = Aх Вычисляется по формуле:
![]()
(напомним, что ln А º logE А, где Е — неперово число). При А = е получим
![]()
4. Производная от логарифмической функции У = logA X вычисляется по формуле
![]()
В частности, при А = е получим
![]()
При вычислении производных пользуются следующими правилами, которые выводятся с помощью правил вычисления пределов (см. гл. VI, §1):*
![]()
* Подразумевается, что все рассматриваемые производные существуют.
Производная от сложной функции F(U(X)) вычисляется по формуле
![]()
Например,
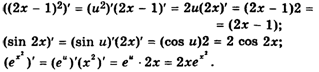
Понятие производной имеет широкие приложения. Как мы уже знаем, производная от пути по времени — это скорость. Но понятие скорости возникает не только при движении. Скорость — важнейшая характеристика многих физических, химических, физиологических и других процессов, происходящих в природе, в человеке, на различных производствах и т. д. И всегда скорость представляет собой производную от некоторой функции.
Производная от скорости называется Ускорением, Она характеризует «скорость изменения скорости». При равноускоренном движении ускорение постоянно, при равномерном оно равно нулю. Если же движение (процесс) описывается некоторой произвольной функцией, то ускорение, вообще говоря, не постоянно и представляет собой столь же важную характеристику, как и скорость.
Другое важное приложение производной — задачи на нахождение наибольших и наименьших (экстремальных) значений. Оно основано на следующем простом факте: если функция принимает в некоторой точке экстремальное значение, и производная в этой точке существует, то она (т. е. производная) равна нулю.
Пример. В тюрьме города Дрюкова собрались строить железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры должна быть не менее 2,5 м, а ее площадь — не менее 6 м2?
Решение. Количество железа пропорционально площади поверхности камеры, которая, как и обыкновенная комната, имеет вид прямоугольного параллелепипеда. Обозначим длину камеры через А, а ширину через B. Тогда пол и потолок имеют площадь АB каждый, две боковые стены по 2,5А, две другие — по 2,5B. Общая площадь получается S = 2Аb + 5А + 5B. При этом, согласно санитарным нормам, АB = 6. Отсюда выразим B и подставим в выражение для 5:
![]()
Итак, мы учли все данные, но величину а еще можно выбирать произвольно, т. е. она является переменной величиной. Ее нужно выбрать так, чтобы значение S получилось наименьшим. Согласно теории, для минимизации функции S(A) следует приравнять нулю производную S'(A). Пользуясь правилами вычисления производных, находим:
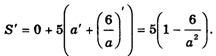
Из уравнения
![]()
Находим, что А = ![]() . При этом значении А площадь будет наименьшей. Она равна S = 12 + 10
. При этом значении А площадь будет наименьшей. Она равна S = 12 + 10![]()
![]() 12 + 10 х 2,45 = 36,5.
12 + 10 х 2,45 = 36,5.
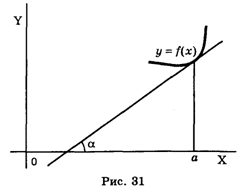
Есть и другие, не менее важные, приложения производной. Например, в геометрии часто используется тот факт, что прозводная от функции У = F(X) в точке Х = А Равна тангенсу угла наклона касательной к графику функции F(X) в точке Х = A: У' = tg a (см. рис. 31).
| < Предыдущая | Следующая > |
|---|