6.1. Идея предела. Предел функции

Идею предельного перехода использовал еще Архимед при вычислении площадей и объемов. Эти вычисле­ния совершенствовались два тысячелетия и привели к созданию дифференциального и интегрального исчисле­ния — наиболее мощного и универсального современно­го математического метода. Этот метод возник в трудах выдающихся ученых Ньютона и Лейбница и развивался усилиями Иоганна I Бернулли, Леонардо Эйлера, Огюстена Коши, Бернгарда Римана, Валле Пуссена, Анри Лебега, Николая Николаевича Лузина, Андрея Никола­евича Колмогорова, Александра Яковлевича Хинчина и многих других.

Предел функции — одно из самых тонких понятий математического анализа. Вы сможете заметить это, внимательно прочитав параграф до конца, в особенности то место, где вычисляются замечательные пределы.

Рассмотрим вначале одну из самых простых функ­ций У = х2. Обычно правую часть в аналитической записи функции обозначают через F(X). Итак, у нас

У = F(X) = х2.

Заметим, что значение этой функции в точке Х0 = 2 будет У0 = 4.

Рассмотрим на оси Х бесконечную последователь­ность точек с координатами

X1 = 2 – 1 = 1; X2 = 2 – ; X3 = 2 – ; ...

Любое из чисел Х1, х2, X3 ... меньше 2-х. Как хорошо видно на рис. 26, эти точки скапливаются около точки X0 = 2. Разности

Уменьшаются (в два раза) и могут стать меньше любого наперед заданного малого положительного числа. По­этому говорят, что бесконечная последовательность чи­сел Х1, х2, X3 ... Стремится к числу 2 или имеет своим Пределом число 2.

Как при этом ведет себя функция У = Х2? Значения переменного У

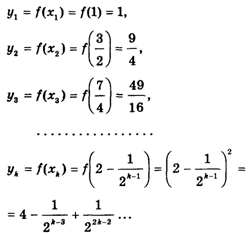
Образуют бесконечную последовательность. С увеличением номера K дроби и стремятся к нулю, поэтому Yk С увеличением номера K стремится к четырем. В этом случае говорят, что предел функции У = х2 при Х, стремящемся к двум, равен четырем, и записывают так:

.

Знак lim есть сокращение от латинского слова Limes, т. е. граница.

Важное замечание. Математики любят придираться к своим результатам и проверяют их до тех пор, пока придраться уже будет не к чему. Такой подход гаранти­рует, что полученный результат является полностью дос­товерным и математически точным, или, как говорят математики, корректным.

Так вот, в наших рассуждениях о пределе имеется существенный пробел. В первом примере мы взяли после­довательность

2 – 1, 2 – , 2 – , 2 – , ...

Но можно было взять, например, и такую:

2 – 1, 2 – , 2 – , 2 – , ...

Которая также имеет своим пределом число 2. Ясно, что таких последовательностей можно указать сколько угодно. Возникает вопрос: зависит ли предел функции от выбора последовательности, т. е. от того, Каким обра­зом переменная Х стремится к заданному значению? Оказывается, что нет, не зависит. Так вот, строгое опре­деление предела функции включает в себя требование независимости от выбора последовательности.

Мы рассмотрели простой пример, когда предел функции в точке X0 равен значению функции в этой точке. В этом случае говорят, что функция Непрерывна в точке X0. Например, функции Kx + B, х2, Eх, sin X являются непрерывными в каждой точке.

Но ценность столь сложных понятий, как последовательность, предел последовательности и предел функции состоит прежде всего в том, что с их помощью можно описывать поведение функций на границе области опре­деления, т. е. при таких значениях переменного Х, в которых функцию определить трудно или невозможно. Рассмотрим, например, функцию

Y = F(X) = ,

Выражающую известный закон обратной пропорциональности. Ее графиком будет гипербола

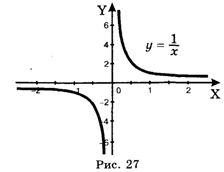
Таблица значений этой функции

Показывает, что если Х стремится к бесконечности (Х® ¥), то У стремится к нулю (У ® 0). Используя по­нятие предела, это можно записать так:

.

Заметим, что выражение «Х стремится к бесконечности» означает, что Х может принять сколь угодно большое значение, или, как еще говорят, стать больше любого наперед заданного числа.

В то же время, если Х уменьшается от единицы до нуля, то получается следующая таблица:

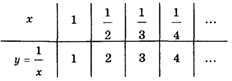
Согласно нашей терминологии,

.

Следующий пример показывает, что для нахождения

Предела иногда нужно проявить некоторую сообразительность. Найдем предел

.

Здесь и числитель, и знаменатель стремятся к бесконеч­ности, поэтому сразу неясно, к чему стремится дробь. Однако, если выполнить простейшее преобразование (раз­делить почленно), то все станет ясно:

Действительно, если Х увеличивается, то дробь уменьшается и стремится к нулю, а, следовательно, разность стремится к единице. Итак, рассматривае­мый предел равен единице.

Еще большую изобретательность нужно проявить, рассматривая предел

.

Здесь сложность состоит в том, что при Х = 1 и числитель и знаменатель обращаются в нуль. Поэтому нельзя найти предел, просто подставив вместо Х единицу (как в первом примере). Но заметим, что, поскольку многочлен, стоящий в числителе, обращается в нуль при Х = 1, то это число бу­дет его корнем. Второй корень равен двум, так что

Х2 – 3Х + 2 = (Х – 1)(Х – 2),

И рассматриваемая функция запишется теперь следую­щим образом:

, .

Сократив на Х – 1, получим функцию G(X) = Х – 2, где Х Может принимать уже любые значения.

Графиком функции У = Х – 2 будет, как мы уже знаем, прямая. А т. к. во всех точках, кроме Х = 1, выполняется тождество F(X) = G(X), то и для заданной функции F(X) гра­фиком также будет прямая, но без точки (Х = 1, Y = –1):

Поэтому

Без доказательства приведем

Правила вычисления пределов

1. Предел суммы нескольких функций равен сумме пределов этих функций.* Например,

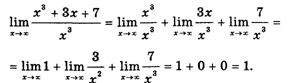
* Здесь, а также в п. 2. подразумевается, что все рассматриваемые пределы существуют.

2. Предел произведения нескольких функций равен произведению пределов этих функций. Например,

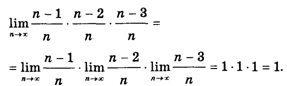
Вычисление сложных пределов — занятие весьма непростое, и для каждого из них приходится придумы­вать свой способ доказательства. Мы рассмотрим только два самых важных, которые называются Замечатель­ными пределами.

Первый замечательный предел: .

Второй замечательный предел: .

Чтобы доказать второе из этих равенств, вспомним, прежде всего, что предел не зависит от выбора последо­вательности значений переменного Х, стремящегося к бесконечности. Составим эту последовательность из на­туральных чисел 1, 2, 3, ... и найдем соответствующие значения функции F(X) = :

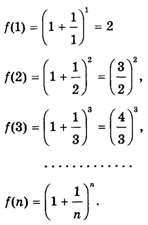
Теперь воспользуемся формулой бинома Ньютона (см. с. 56):

Подставляя сюда А = 1 и B = , мы получим следующее:

Каждая из дробей , , ... меньше единицы. Поэтому, если в последней сумме эти дроби заме­нить единицами, то получим число, большее F(N):

Заметим, что правая часть этого неравенства есть в точ­ности сумма первых П слагаемых того самого ряда, с по­мощью которого мы определили в гл. I неперово число:

Поэтому, устремляя в неравенстве (2) П к бесконечности, мы получим:*

* Обратите внимание, что из Строгого неравенства (2) в результате предельного перехода получилось Нестрогое неравен­ство (3). Это следствие одной из теорем теории пределов: если F(X) < G(X) то .

Вернемся теперь снова к сумме (1). В ней все слагаемые — числа положительные, поэтому, если часть пос­ледних слагаемых отбросить и оставить только K пер­вых, то сумма уменьшится:

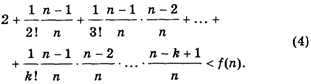
Устремим в этом неравенстве N к бесконечности. Так как каждая из дробей , , ... стремится при этом к единице, то в результате получится такое неравенство:

Из наших рассуждений вытекает, что K — число слагаемых слева — может быть любым, поэтому неравенство сохранится, если K устремить к бесконечности! Но тогда слева снова получится бесконечный ряд, т. е. неперово число Е. Таким образом, мы приходим к неравенству

Из неравенств (3) и (5) следует, что

Что и требовалось доказать.

Первый замечательный предел получается из геометрических соображений. Рассмотрим окружность единичного радиуса и вспомним, что по определению (см. рис. 29) |АМ| = sin X, |BN| = tg Х, а длина дуги AN в радианах равна Х. Для определенности мы считаем, что > х > 0. В случае, если Х < 0, рассуждения будут аналогичными.

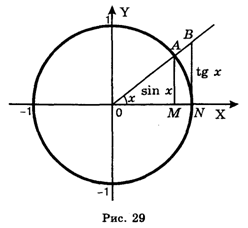
Рассмотрим очевидное неравенство |АМ| < |AN|. Так как длина хорды АN меньше длины дуги AN, то sin Х £ х. Разделив на Х, получим

Отсюда

Далее заметим, что площадь сектора OAN меньше пло­щади треугольника OBN. Это приводит к неравенству R2X £ R2 tg Х или Х < tg Х (равенство достигается при Х = 0). Разделив на Х, получим

Теперь устремим Х к нулю. Так как предел произведе­ния равен произведению пределов, то

Но

Поэтому последнее неравенство перепишется так:

Сравнивая с неравенством (6), приходим к единственно­му возможному варианту:

Что и требовалось доказать.

Пользуясь пер­вым замечательным пределом, выведем формулу для вычис­ления площади кру­га. Впишем в круг радиуса R правиль­ный N-угольник А1А2...Ап и найдем его площадь Sn. Как видно из рисунка, Sn = NS, где S— Площадь треуголь­ника OA1A2 . Но

Поэтому

Площадью S круга называется предел последовательности Sn. Пользуясь первым замечательным пределом, получаем:

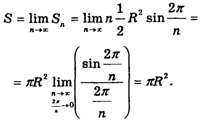
УПРАЖНЕНИЯ

1. Найдите следующие пределы:

Важное замечание. Теория пределов позволяет уточнить понятие бесконечной десятичной дроби (см. гл. I, §1), рассматривая ее как Предел последовательности десятичных приближений. Например, число является пределом последовательности 0.3, 0.33, 0.333, ..., а чис­ло есть предел последовательности 1, 1.4, 1.41, 1.414, ... (см. там же).

< Предыдущая		Следующая >