146. Вычисление площади поверхности вращения

Дифференциал площади поверхности, полученный при вращении дуги плоской кривой вокруг оси Ох, записывают как:

.

Площадь всей поверхности вычисляют по формуле:

.

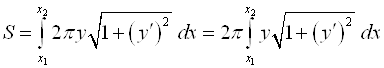При вращении дуги вокруг оси Оу площадь поверхности равна: .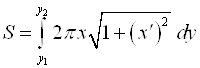

Пример 31. Найдите площадь поверхности, которая получена при вращении дуги кубической параболы вокруг оси между прямыми и .

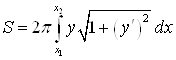Решение. При вращении дуги кривой вокруг оси используем формулу . Получим: .

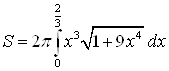Для вычисления интеграла введем новую переменную: , тогда , а пределы интегрирования будут равны: , .

.

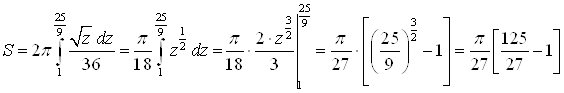Ответ. .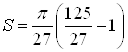

< Предыдущая		Следующая >