145. Вычисление объема тела вращения

Если тело получено путем вращения криволинейной трапеции ABCD вокруг оси Ох (рисунок 4.5), то любое его плоское сечение, перпендикулярное оси Ох, будет представлять собой круг. Радиус этого круга будет равен ординате кривой .

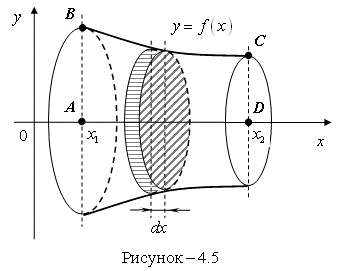
Площадь сечения , которое соответствует абсциссе Х, будет равна . Элементарный объем, который соответствует приращению , будет равен объему элементарного цилиндра .

Весь объем тела вращения определяется формулой:

.

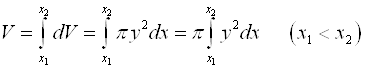Если тело получено вращением вокруг оси Оу, то:

.

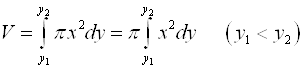Пример 30. Найдите объем тела, которое образовано вращением криволинейной трапеции вокруг оси , если , .

Решение. Построим параболу и прямые и . При вращении вокруг оси мы получим часть параболоида вращения. Его объем будем вычислять по формуле 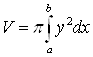. Тогда получим:

.

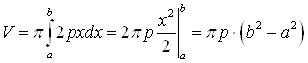Ответ. .

< Предыдущая		Следующая >