144. Вычисление длины дуги плоской кривой

Длина кривой линии – это предел, к которому стремится длина вписанной в нее (или описанной) ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из них к нулю.

В прямоугольной системе координат дифференциал длины линии равен , а длина дуги вычисляется по формуле:

.

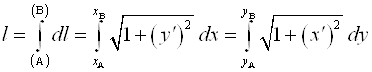Пример 29. Найдите длину дуги окружности между точками и .

Решение. По формуле длины дуги найдем: . (*)

Из уравнения окружности найдем, что , а производная . (**)

Подставим значение производной (**) в формулу (*).

.

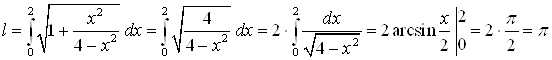Проверка. Мы знаем, что длина окружности равна . При длина всей окружности . В нашей задаче уравнение описывает окружность радиуса с центром в начале координат. Длина дуги окружности от до составляет часть длины всей окружности, значит: .

Ответ. Длина дуги окружности равна .

< Предыдущая		Следующая >