143. Вычисление площади плоской фигуры

Площадь плоской фигуры определяется по формуле:

.

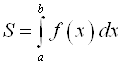При решении некоторых задач целесообразно использовать следующий порядок действий:

1. Выполнить чертеж.

2. Найти пределы интегрирования.

3. Вычислить площадь плоской фигуры.

Пример 26. Вычислите площадь фигуры, ограниченной кривой линией прямыми линиями , и осью .

Решение.

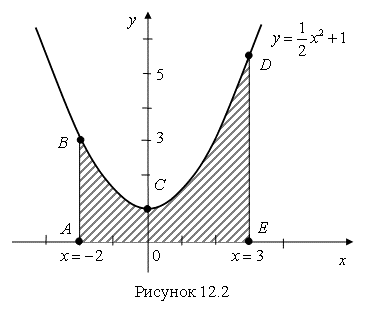
1) Выполним чертеж. Для этого в системе координат ХОу построим графики заданных формулами функций. Из рисунка 12.2 мы видим, что необходимо вычислить площадь криволинейной трапеции АВСDЕ.

2) Пределы интегрирования определим как пределы изменения аргумента . Кривая ВСD пересекается с прямой в точке , а с прямой В точке 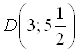. Мы видим, что минимальное значение аргумент принимает в точке В, где , а максимальное значение – в точке D, где . Значит, нижний предел интегрирования , а верхний предел .

3) Вычислим площадь по формуле 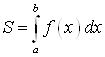. Тогда:

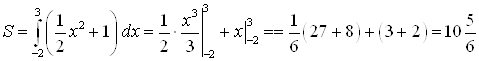кв. ед.

Ответ. Площадь криволинейной трапеции равна квадратных единиц.

Пример 27. Вычислите площадь фигуры, ограниченной кривой и осью на полупериоде изменения аргумента .

Решение.

1. Построим график функции на полупериоде изменения аргумента .

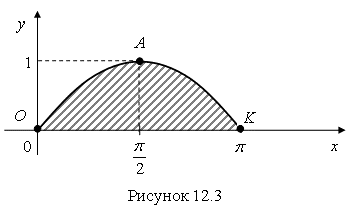
Нам необходимо вычислить площадь криволинейной трапеции OАК (рис. 12.3).

2. Нижний предел интегрирования , а верхний предел .

3. Площадь вычислим по формуле: .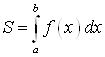

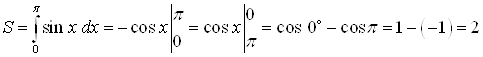кв. ед.

Ответ. Площадь фигуры составляет 2 квадратные единицы.

Пример 28. Вычислите площадь фигуры, ограниченной кривой и прямой

Решение. 1. Построим графики функций и

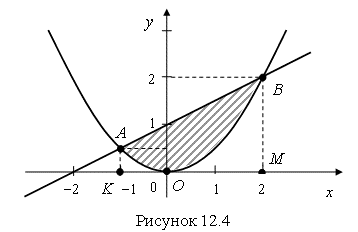
Необходимо найти площадь криволинейной трапеции АВО (рис. 12.4).

2. Найти пределы интегрирования можно, если решить совместно систему уравнений: , тогда , откуда .

Решением этого уравнения есть координаты (абсциссы) точек пересечения графиков функций. Эти координаты равны и .

Нижним пределом интегрирования будет , а верхним будет .

3. Площадь криволинейной трапеции будет равна разности площади трапеции и площади трапеции : .

Площадь трапеции кв. ед.

Площадь трапеции кв. ед.

кв. ед.

Ответ. Площадь трапеции АВО равна квадратных единиц.

< Предыдущая		Следующая >