142. Методы определенного интегрирования
Правила неопределенного интегрирования можно применить для вычисления определенного интеграла.
Формула интегрирования по частям для определенного интеграла будет следующей:
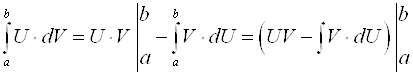 .
.
Пример 20. Найдите интеграл 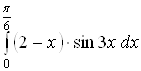 .
.
Решение. Обозначим ![]() , а
, а ![]() .
.
Найдем, что ![]() , а
, а ![]() .
.
Используем формулу интегрирования по частям:
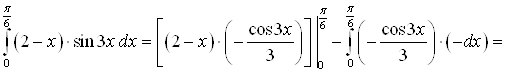

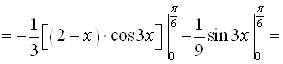
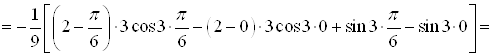
![]() .
.
Ответ. 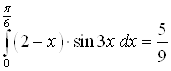 =
=![]() .
.
Пример 21. Вычислите интеграл 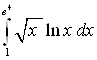 .
.
Решение. Обозначим ![]() , а
, а ![]() . Найдем
. Найдем ![]() и
и  .
.
Используем формулу интегрирования по частям:

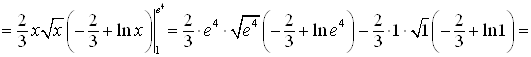
![]() .
.
Ответ. 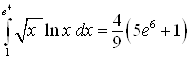 .
.
Формула замены переменной для определенных интегралов принимает вид: 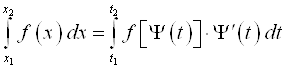 , где
, где ![]() – непрерывная и дифференцируемая на интервале
– непрерывная и дифференцируемая на интервале ![]() функция. При этом интервал
функция. При этом интервал ![]() не может быть ýже интервала
не может быть ýже интервала ![]() , в котором интегрируется непрерывная функция
, в котором интегрируется непрерывная функция ![]() .
.
Из этой формулы видно, что подынтегральное выражение преобразуется так же, как при замене переменной в неопределенном интеграле. Старые пределы интегрирования ![]() и
и ![]() связаны с новыми пределами интегрирования
связаны с новыми пределами интегрирования ![]() и
и ![]() так же, как старая переменная
так же, как старая переменная ![]() с новой переменной
с новой переменной ![]() .
.
Пример 22. Найдите определенный интеграл 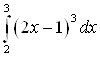 .
.
Решение. Введем новую переменную: ![]() , тогда
, тогда ![]() , откуда
, откуда ![]() . Новые пределы интегрирования будут следующие:
. Новые пределы интегрирования будут следующие:
При ![]() ,
, ![]() ; при
; при ![]() ,
, ![]() .
.
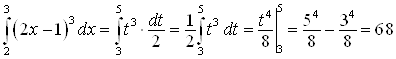 .
.
Ответ. 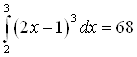 .
.
Для замены переменной в определенном интеграле часто используют формулу ![]() . Тогда новые пределы интегрирова-ния
. Тогда новые пределы интегрирова-ния ![]() и
и ![]() определяются по формулам
определяются по формулам ![]() , а
, а ![]() .
.
Пример 23. Найдите интеграл 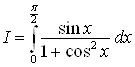 .
.
Решение. Введем новую переменную ![]() . Тогда
. Тогда ![]() , а пределы интегрирования вычисляем так:
, а пределы интегрирования вычисляем так: ![]() ,
, ![]() .
.
Перепишем интеграл с новой переменной и вычислим его.
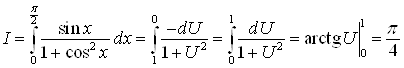 .
.
Ответ. 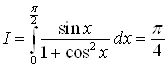 .
.
Можно показать, что определенный интеграл по симметрич-ному пределу ![]() равен нулю, если подынтегральная функция нечетная, и равен
равен нулю, если подынтегральная функция нечетная, и равен 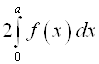 , если подынтегральная функция четная:
, если подынтегральная функция четная: 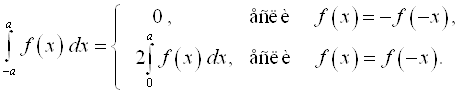
Пример 24. Найдите интеграл 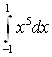 .
.
Решение. Подынтегральная функция нечетная, так как ![]() , значит
, значит 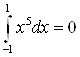 . Сделаем проверку.
. Сделаем проверку.
Проверка. Найдем интеграл, используя формулу Ньютона-Лейбница:
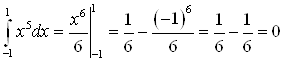 .
.
Ответ. 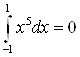 .
.
Пример 25. Найдите интеграл 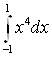 .
.
Решение. Подынтегральная функция ![]() четная, значит,
четная, значит,
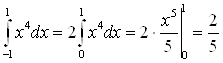 .
.
Проверка. Найдем интеграл, используя формулу Ньютона-Лейбница:
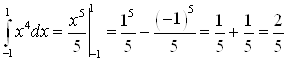 .
.
Ответ. 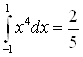 .
.
Ответьте на вопросы
1. Напишите формулу интегрирования по частям для определенного интеграла.
2. Как преобразовать подынтегральное выражение при замене переменной?
3. Как найти новые пределы интегрирования?
4. Чему равен определенный интеграл по симметричному пределу?
| < Предыдущая | Следующая > |
|---|