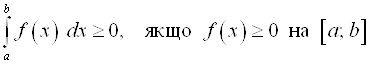141. Понятие определенного интеграла и его основные свойства

В системе координат рассмотрим плоскую фигуру ABCD (рис. 12.1). Эта фигура называется Криволинейной трапецией.

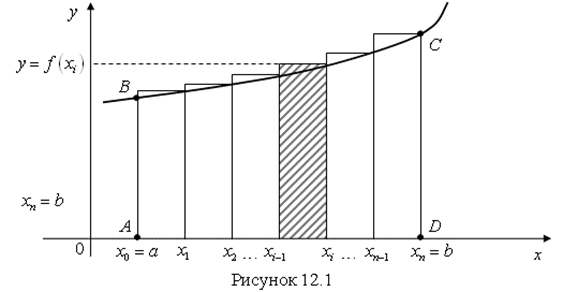
Криволинейная трапеция – это фигура, которая ограничена осью Оx, линией и двумя прямыми и .

Любая прямая, параллельная оси Оу, пересекает линию только в одной точке.

Интервал оси Оx называется Основанием криволиней-ной трапеции. Разобьем интервал на N частей точками ... , и на каждом новом интервале построим прямоугольник с основанием и высотой . Площадь I-го прямоугольника равна , а сумма всех площадей:

.

При () площадь криволинейной трапеции равна . При этом предел не зависит от способа деления интервала на части, необходимо только, чтобы наибольший из Стремился к нулю.

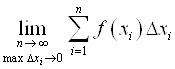Теорема. Для любой функции , непрерывной на , существует предел и этот предел не зависит от способа разбиения интервала и от выбора точек разбиения .

Сумма 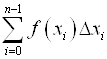называется Интегральной Суммой функции на интервале .

Операция нахождения предела этой суммы называется Интегрированием функции на интервале.

Предел интегральной суммы называется Определенным интегралом функции на интервале : .

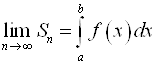Следовательно, площадь криволинейной трапеции находят по формуле: 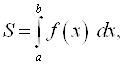где А – нижний предел интегрирования; B – верхний предел интегрирования; – интервал интегрирования.

Свойства определенных интегралов

1. .

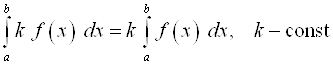2. .

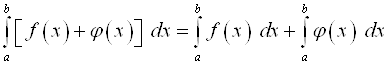3. .

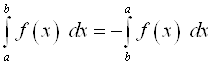4. , .

5. .

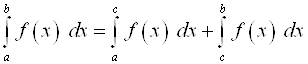6. .

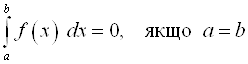Для вычисления определенных интегралов применяют основную формулу интегрального исчисления – формулу Ньютона–Лейбница: 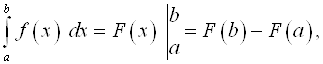где – первообразная функции

Надо подчеркнуть, что неопределенный интеграл – Функция, определенный интеграл – Число.

Пример 18. Вычислите определенный интеграл .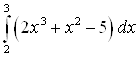

Решение. Найдем первообразную подынтегральной функции:

.

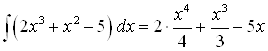Используем формулу Ньютона-Лейбница:

.

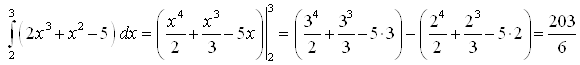Ответ. .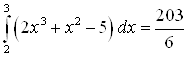

Пример 19. Вычислите определенный интеграл .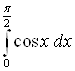

Решение. Найдем первообразную подынтегральной функции и используем формулу Ньютона-Лейбница:

.

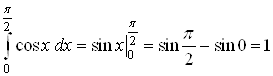Ответ. .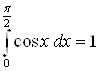

Ответьте на вопросы

1. Какая фигура называется криволинейной трапецией?

2. Что является основанием трапеции?

3. Сколько точек пересечения с графиком кривой может иметь любая прямая, параллельная оси Оу в
интервале ?

4. Как называется выражение ?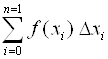

5. Как называется предел интегральной суммы ?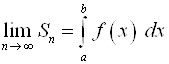

6. Чему равна площадь криволинейной трапеции?

< Предыдущая		Следующая >