140. Основные методы интегрирования
Рассмотрим некоторые методы интегрирования.
Замена переменной интегрирования (подстановка) является одним из важнейших методов вычисления интегралов.
Первый метод (Интегрирование методом замены перемен-ной). Если известно, что ![]() , то справедливо равенство
, то справедливо равенство ![]() где
где ![]() – дифференцируемая функция.
– дифференцируемая функция.
Пример 3. Найдите интеграл ![]() .
.
Решение. Сделаем замену переменной: ![]() , тогда
, тогда ![]() , а
, а ![]() Интеграл принимает вид табличного интеграла:
Интеграл принимает вид табличного интеграла:
![]() .
.
Ответ. ![]() .
.
Пример 4. Найдите интеграл ![]() .
.
Решение. Сделаем замену: ![]() , и найдем
, и найдем ![]() , тогда
, тогда
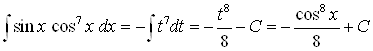 .
.
Ответ. 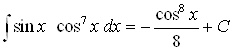 .
.
Пример 5. Найдите интеграл ![]() .
.
Решение. Сделаем замену: ![]() , и найдем
, и найдем ![]() , тогда
, тогда
![]() .
.
Ответ. ![]() .
.
Пример 6. Найдите интеграл 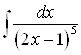 .
.
Решение. Сделаем замену: ![]() , откуда получим
, откуда получим ![]() , тогда
, тогда 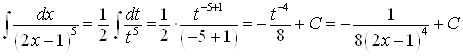 .
.
Ответ. 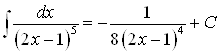 .
.
Пример 7. Найдите интеграл 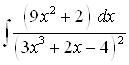 .
.
Решение. Сделаем замену: ![]() , тогда
, тогда ![]() . Получим:
. Получим:  .
.
Ответ. 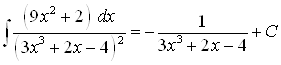 .
.
Второй метод (Метод разложения).
Если ![]() , а
, а ![]() И
И ![]() Имеют первообразные, то
Имеют первообразные, то
![]() .
.
Пример 8. Найдите интеграл ![]() .
.
Решение. Запишем этот интеграл как алгебраическую сумму интегралов и найдем каждый из них отдельно: ![]()
![]()
Проверка. Возьмем производную от полученного результата:
 .
.
Мы получили подынтегральную функцию. Значит, решение правильное.
Ответ. ![]() .
.
Пример 9. Найдите интеграл 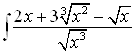 .
.
Решение. Преобразуем подынтегральную функцию, для чего разделим каждый член многочлена числителя на знаменатель и запишем результат как сумму интегралов:


Ответ.  .
.
Если в подынтегральной функции наибольший показатель степени многочлена в числителе равен наибольшему показателю степени многочлена в знаменателе, то необходимо разделить числитель на знаменатель и представить интеграл в виде алгебраической суммы интегралов.
Пример 10. Найдите интеграл ![]() .
.
Решение. Преобразуем подынтегральную функцию так, чтобы выделить целую часть дроби. Для этого в числителе прибавим и вычтем 4:
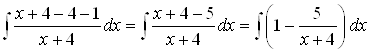 .
.
Полученный интеграл представим в виде суммы интегралов:
![]() .
.
Здесь, ![]() , потому что
, потому что ![]() .
.
Ответ. ![]() .
.
Если числитель дроби подынтегральной функции – это постоянное число, а знаменатель – это квадратный трехчлен, то знаменатель можно дополнить до полного квадрата, и интеграл сводится к табличному интегралу вида:
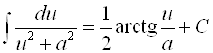 или
или 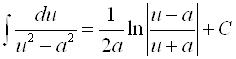 .
.
Пример 11. Найдите интеграл ![]() .
.
Решение. В знаменателе дроби прибавим и вычтем 4, тогда интеграл будет иметь вид: ![]()
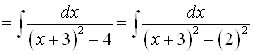 .
.
Перейдем к новой переменной ![]() , тогда
, тогда ![]() и интеграл перепишем так:
и интеграл перепишем так: 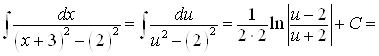
![]() .
.
Ответ. ![]() .
.
Пример 12. Найдите интеграл ![]() .
.
Решение. Преобразуем знаменатель и перепишем интеграл в виде:
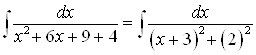 . Перейдем к новой переменной
. Перейдем к новой переменной ![]() ,
,
Тогда: 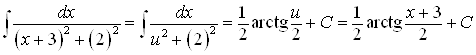 .
.
Ответ. ![]() .
.
Третий метод (Интегрирование по частям). Формула интегрирования по частям имеет вид: ![]() .
.
Пример 13. Найдите ![]() .
.
Решение. Обозначим ![]() ,
, ![]() , тогда
, тогда ![]() ,
, ![]() .
.
Из формулы интегрирования по частям имеем:
![]() .
.
Ответ. ![]() .
.
Интегралы вида ![]()
![]()
![]() где
где ![]() – многочлен, можно взять по частям, если
– многочлен, можно взять по частям, если ![]() обозначить через
обозначить через ![]() .
.
Пример 14. Найдите ![]() .
.
Решение. Обозначим: ![]()
![]() тогда
тогда ![]()
![]() .
.
Из формулы интегрирования по частям имеем:
![]() .
.
Ответ. ![]() .
.
Интегралы вида ![]()
![]()
![]()
![]() где
где ![]() – многочлен от
– многочлен от ![]() , можно взять по частям, если обозначить
, можно взять по частям, если обозначить ![]() .
.
Пример 15. Найдите ![]()
Решение. Обозначим: ![]()
![]() тогда
тогда ![]()
![]() . Из формулы интегрирования по частям имеем:
. Из формулы интегрирования по частям имеем:
![]()

Ответ. 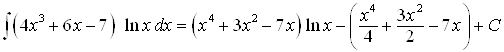 .
.
Четвертый метод (интегрирование рациональных функций). Рациональные функции всегда интегрируются в элементарных функциях. Целая рациональная функция (многочлен) интегрируется так:
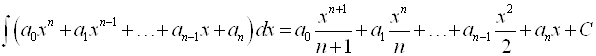 .
.
Интеграл дробной рациональной функции можно найти, представив его как сумму элементарных слагаемых.
Если степень многочлена числителя ![]() больше или равна степени многочлена знаменателя, то, разделив многочлен
больше или равна степени многочлена знаменателя, то, разделив многочлен ![]() на многочлен
на многочлен ![]() , получим целую рациональную функцию
, получим целую рациональную функцию ![]() и дробно-рациональную функцию
и дробно-рациональную функцию 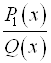 . Степень многочлена
. Степень многочлена ![]() будет меньше степени многочлена
будет меньше степени многочлена ![]() :
:
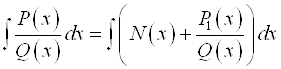 .
.
Интегрирование целой рациональной функции не составляет трудностей, а правильную рациональную дробь можно представить как сумму элементарных, всегда интегрируемых дробей следующих двух видов: 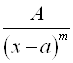 и
и 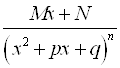 , где M и N – целые положительные числа.
, где M и N – целые положительные числа.
Для того чтобы представить правильную рациональную дробь в виде суммы элементарных дробей, необходимо разложить ее знаменатель ![]() на простейшие множители.
на простейшие множители.
1. Если уравнение ![]() имеет только действительные корни, и они разные, то получим все слагаемые вида
имеет только действительные корни, и они разные, то получим все слагаемые вида 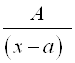 :
:
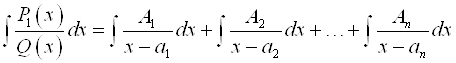 .
.
2. Если уравнение ![]() имеет только действительные, но кратные корни, кратности
имеет только действительные, но кратные корни, кратности ![]() , тогда:
, тогда:
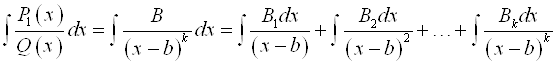 .
.
3. Если уравнение ![]() не имеет действительных корней, но имеет одну пару комплексных сопряженных чисел
не имеет действительных корней, но имеет одну пару комплексных сопряженных чисел ![]() , тогда
, тогда 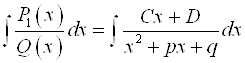 .
.
4. Если уравнение ![]() имеет пары комплексных сопряженных чисел кратности T, тогда:
имеет пары комплексных сопряженных чисел кратности T, тогда:
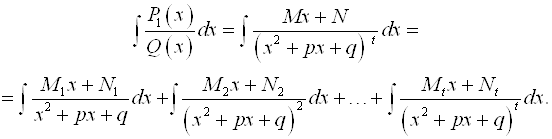
В вышеприведенные формулы входят неопределенные коэффициенты A, B, C, D, M и N. Для определения этих коэффициентов нужно составить систему уравнений, используя равенства коэффициентов при одинаковых степенях переменной Х в левой и правой частях данных формул.
В общем случае уравнение ![]() может иметь действительные и комплексно-сопряженные корни одновременно, и тогда в разложении правильной рациональной дроби будут присутствовать слагаемые всех приведенных видов.
может иметь действительные и комплексно-сопряженные корни одновременно, и тогда в разложении правильной рациональной дроби будут присутствовать слагаемые всех приведенных видов.
Методику интегрирования дробно-рациональных функций рассмотрим на примерах.
Пример 16. Найдите интеграл 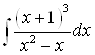 .
.
Решение. Данная подынтегральная функция – это неправильная дробь (наибольшая степень переменной ![]() в числителе равна 3, а наибольшая степень переменной
в числителе равна 3, а наибольшая степень переменной ![]() в знаменателе равна 2). Выделим целую часть дроби, для этого разделим числитель дроби
в знаменателе равна 2). Выделим целую часть дроби, для этого разделим числитель дроби ![]() на знаменатель дроби
на знаменатель дроби ![]() , получим:
, получим:

Подынтегральное выражение представим в виде:
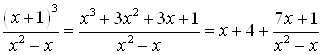 .
.
Так как корни уравнения ![]() – Это разные действительные числа
– Это разные действительные числа ![]() ,
, ![]() , то правильную дробь
, то правильную дробь ![]() представим как сумму слагаемых:
представим как сумму слагаемых: 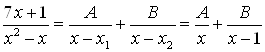 .
.
Найдем неизвестные коэффициенты А и В, для этого приравняем коэффициенты при одинаковых степенях переменной ![]() в полученном равенстве. Приведем к общему знаменателю правую часть последнего равенства:
в полученном равенстве. Приведем к общему знаменателю правую часть последнего равенства:

В равенстве 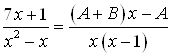 знаменатель в левой и правой части одинаков:
знаменатель в левой и правой части одинаков: ![]() . Для того чтобы дроби были равны, числители тоже должны быть равны:
. Для того чтобы дроби были равны, числители тоже должны быть равны: ![]() . Поэтому,
. Поэтому, ![]() и
и ![]() . Мы получили систему двух уравнений, из которой и найдем коэффициенты
. Мы получили систему двух уравнений, из которой и найдем коэффициенты ![]() и
и ![]() :
: 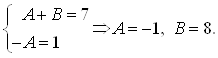 Значит,
Значит, ![]() , а все подынтегральное выражение можно записать так:
, а все подынтегральное выражение можно записать так:
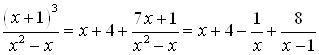 .
.
Таким образом, заданный интеграл можно представить в виде суммы интегралов, которые легко вычислить:
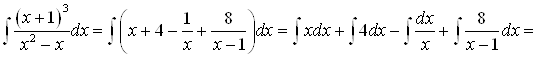
![]() .
.
Проверка. Возьмем производную от полученного выражения:

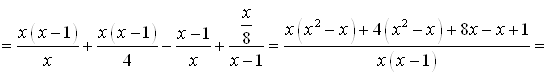
 .
.
Полученное выражение 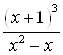 – это подынтегральная функция. Интеграл найден правильно.
– это подынтегральная функция. Интеграл найден правильно.
Ответ. 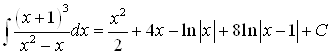 .
.
Пример 17. Найдите интеграл 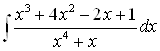 .
.
Решение. Подынтегральное выражение представляет собой правильную дробь. Разложим знаменатель дроби ![]() на множители и приравняем его к нулю:
на множители и приравняем его к нулю: ![]() . Корнями данного уравнения будут два действительных числа:
. Корнями данного уравнения будут два действительных числа: ![]() ,
, ![]() и пара комплексных сопряженных чисел:
и пара комплексных сопряженных чисел: ![]() . Поэтому подынтегральную дробь можно представить в виде суммы элементарных дробей:
. Поэтому подынтегральную дробь можно представить в виде суммы элементарных дробей:
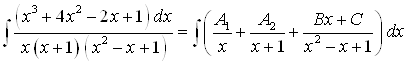 . (*)
. (*)
Приравняем подынтегральные выражения левой и правой части полученного выражения:
 .
.
После преобразований получим:
 .
.
Умножим левую и правую часть равенства на ![]() , тогда
, тогда ![]() .
.
Приравнивая коэффициенты при одинаковых степенях ![]() , мы получим четыре уравнения, из которых найдем
, мы получим четыре уравнения, из которых найдем ![]() и
и ![]() :
:

Решением этой системы уравнений будет: ![]() .
.
Подставим полученные значения ![]() и
и ![]() в формулу (*):
в формулу (*):
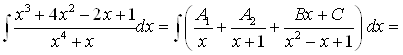
 .
.
Найдем каждый из интегралов отдельно.
Первый интеграл – это табличный интеграл: ![]() .
.
Во втором интеграле ![]() сделаем замену переменной
сделаем замену переменной ![]() , тогда
, тогда ![]() и получим табличный интеграл относительно
и получим табличный интеграл относительно ![]() :
:
![]() .
.
В третьем интеграле ![]() в числителе прибавим и вычтем 1, тогда:
в числителе прибавим и вычтем 1, тогда: ![]() .
.
В интеграле ![]() введем новую переменную
введем новую переменную ![]() , получим
, получим ![]() , тогда:
, тогда: ![]() .
.
Интеграл 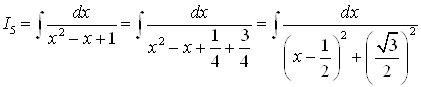 .
.
Если в интеграле ![]() обозначить
обозначить ![]() , тогда
, тогда ![]() и получим:
и получим:

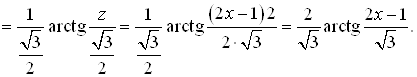
Найдем 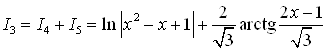 . Теперь мы можем записать, что
. Теперь мы можем записать, что 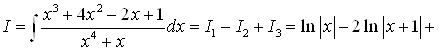
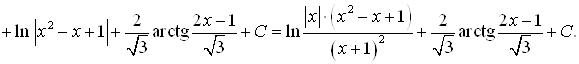
Ответ. 
Ответьте на вопросы
1. Какие основные методы интегрирования вы знаете?
2. Какие приемы применяют при использовании метода разложения?
3. Напишите формулу интегрирования по частям.
4. Что обозначить через U, а что через DV в интеграле вида ![]() и интегралах вида
и интегралах вида ![]() ?
?
5. Когда используется метод замены переменной при интегрировании?
| < Предыдущая | Следующая > |
|---|