139. Основные свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен его подынтегральному выражению: .

2. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

.

Значит, дифференцирование и интегрирование являются взаимно обратными действиями.

3. Постоянный множитель можно вынести за знак неопре-деленного интеграла: .

4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от слагаемых: .

5. Все формулы интегрирования сохраняют свой вид, если вместо независимой переменной подставлять в них любую дифференцируемую функцию от этой переменной.

Если , то ,

Где – любая дифференцируемая функция от .

Пример 1. Найдите интеграл .

Решение. Мы знаем, что есть производная от , поэтому перепишем интеграл так: .

Здесь , а . Полученный интеграл будет табличным: .

Ответ. .

Пример 2. Найдите интеграл .

Решение. Умножим и разделим интеграл на (–5) и внесем множитель (–5) под знак интеграла .

Обозначим , тогда получим табличный интеграл .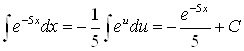

Ответ. .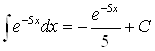

Как показывают примеры, для вычисления интегралов сложных подынтегральных выражений, необходимо подынтегральное выражение преобразовать так, чтобы оно приняло вид подынтегрального выражения одного из табличных интегралов.

Ответьте на вопросы

1. Чему равен дифференциал от неопределенного интеграла?

2. Чему равен интеграл от дифференциала функции?

3. Напишите формулу интеграла от алгебраической суммы функций.

4. Как изменятся формулы интегрирования, если независимую переменную заменить дифференцируемой функцией от этой переменной?

5. Можно ли вынести постоянный множитель за знак интеграла?

< Предыдущая		Следующая >